이전 질문 게시판은 새 글 쓰기를 막았습니다. [질문 게시판]을 이용바랍니다.
| Date |
2009/03/23 03:28:00 |
| Name |
Eternity |
| File #1 |
answer.JPG (18.1 KB), Download : 10 |
| File #2 |
answer2.JPG (16.8 KB), Download : 7 |
| Subject |
45301 문제의 해 한번 올려봅니다. |
질문에 대한 답인 만큼, 댓글로 달아야 함이 도리이겠으나...
그림이 들어간 설명이 필요한 관계로... 별도 글을 쓰게 된 점 양해 부탁드리겠습니다.
그런데.. 제 머리로는... 중1 교과과정만으로 해를 쓰기는 불가능하네요.
제 기억으로는 중1 과정에서 '한 변의 길이가 주어진 정삼각형의 넓이'를 배우지 않았던 듯 한데요.
제가 쓴 풀이에는 삼각함수까지 들어가지는 않습니다만...
정삼각형의 넓이를 구할 수 없으면 성립이 되지 않는 풀이인지라....
그래도 일단 써 보겠습니다.
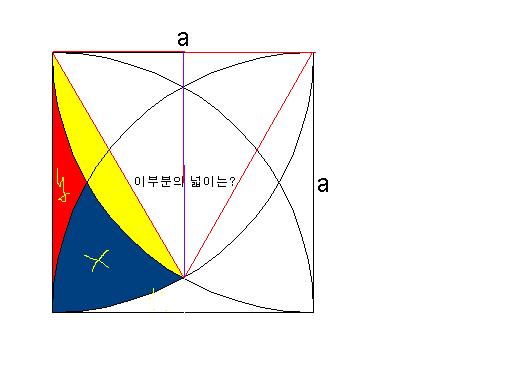
먼저... 붉은 선으로 이루어진 삼각형은 정삼각형입니다.
세 변의 길이가 모두 같기 때문입니다.
(정사각형의 꼭지점에서 두 부채꼴의 호의 교점을 연결한 선분이 동일한 부채꼴의 반지름이기 때문이지요.)
그리고... 중심각의 크기가 60도인 부채꼴의 넓이에서.. 붉은 선으로 이루어진 정삼각형의 넓이를 뺍니다.
(그림에서의 노란 부분입니다.)
그리고.. 각의 크기가 30도인 부채꼴의 넓이에서 노란부분을 뺀 부분을 x + y 라고 가정하겠습니다.
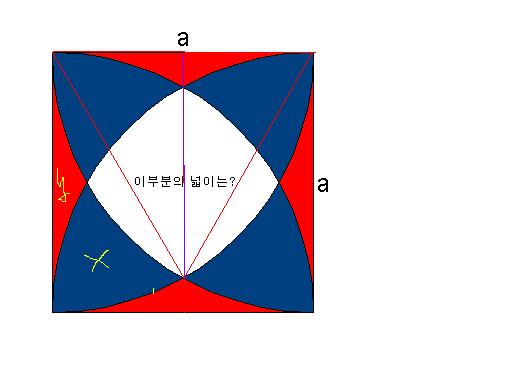
그런데... 이 문제의 답을 z라고 가정한다면...
문제의 정사각형의 넓이는 4x + 4y + z 가 됩니다.
그런데 이 정사각형의 넓이는 a^2이므로...
a^2 - 4 * (x + y)를 하게 되면 z를 구할 수 있습니다.
한 변의 길이가 주어진 정삼각형의 넓이를 구할 수 있다면
굳이 삼각함수를 동원하지 않아도 풀 수 있는 문제입니다만...
정삼각형의 넓이 공식 자체가 삼각함수의 개념을 익히지 않은 상태에서는 무의미한지라...
이 풀이가 도움이 될지 모르겠습니다. 단순히 중1 교과과정만을 근거로 풀이를 쓰기에는 무리가 있는 것으로 보입니다.
|
통합규정 1.3 이용안내 인용
"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.
법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
|