|
:: 게시판
:: 이전 게시판
|
- PGR21 관련된 질문 및 건의는 [건의 게시판]을 이용바랍니다.
- (2013년 3월 이전) 오래된 질문글은 [이전 질문 게시판]에 있습니다. 통합 규정을 준수해 주십시오. (2015.12.25.)
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
16/04/13 01:54
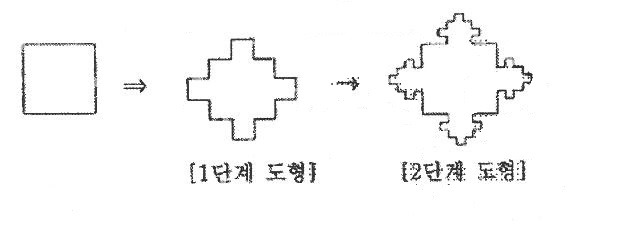
i번째 만들어진 정사각형의 개수 := n(i)
=> i+1번째 만들어진 정사각형의 개수 = 3*n(i) => i번째 만들어진 정사각형 개수 (i>0) := (1+3)*3^(i-1) i번째 만들어진 정사각형 한 개의 넓이 := s(i) => i+1번째 만들어진 정사각형 한 개의 넓이 := s(i)/9 => i번째 만들어진 정사각형 한 개의 넓이 = 2*2/9^i => Bn = 2*2 + sum( 4*3^(n-1) * 4/9^n ), (n>0) i번째 만들어진 정사각형 한 변의 길이 := l(i) = 2/3^i => i+1 번째 만들어진 정사각형 한 개로 인해 늘어난 길이 = 2*l(i)/3 = 4 / 3^(i+1) => An = 2*4 + sum( 4*3^(n-1) * 4/3^(n+1) ), (n>0) 흠.. 생각나는대로 끄적여봤는데 어딘가 틀렸을 확률이 커요;
16/04/13 02:20
#1
T(1) = A(n)-A(n-1)으로 놓았을 때 T(1) = (4)*(2*1/3)*(2) T(2) = (4*3)*(2*1/3^2)*(2) T(3) = (4*3^2)*(2*1/3^3)*(2) ... T(n) = (4*3^(n-1))*(2*1/3^n)*(2) = 16/3 [(이번 단계에서 새로 생긴 사각형의 개수)*(이번 단계에서 지워진 변 하나의 길이)*(지워진 변이 돌기로 변하면서 증가하는 길이의 순이율 = +3-1] A(n) = A(0)+∑T(n) = 8+∑16/3 = 8+16n/3 n을 양의 무한으로 보낼 때 A(n)은 양의 무한으로 발산 #2 R(n) = B(n)-B(n-1)으로 놓았을 때 R(1) = (4*1/9)*(4) R(2) = (4*1/9^2)*(4*3) R(3) = (4*1/9^3)*(4*3^2) ... R(n) = (4*1/9^n)*(4*3^(n-1)) = (16/3)*(1/3)^n [(이번 단계에서 새로 생긴 정사각형의 개당 면적)*(이번 단계에서 새로 생긴 정사각형의 개수)] B(n) = B(0)+∑R(n) = 4+(16/3)∑(1/3)^n = 4+(8/3)(1-1/3^n) n을 양의 무한으로 보낼 때 B(n)은 20/3으로 수렴 급하게 풀어봤는데 맞을런지 모르겠네요. 검토좀ㅠ
|
||||||||||||