|
:: 게시판
:: 이전 게시판
|
- PGR21 관련된 질문 및 건의는 [건의 게시판]을 이용바랍니다.
- (2013년 3월 이전) 오래된 질문글은 [이전 질문 게시판]에 있습니다. 통합 규정을 준수해 주십시오. (2015.12.25.)
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
16/05/17 16:21
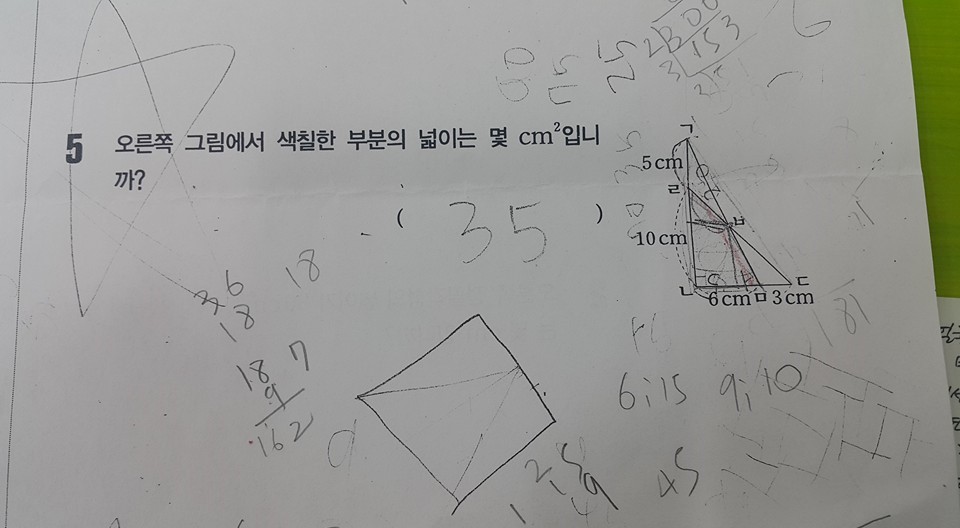
비읍에서 기역니은에 내린 수선을 시옷, 니은디귿에 내린 수선을 이응이라고 하고
비읍시옷의 길이를 a, 비읍이응의 길이를 b라고 하면 넓이는 ab+1/2a(10-b)+1/2b(6-a) = 5a+3b가 됩니다. 그리고 직각삼각형이기 때문에 (5+10-b) : a = 15 : 6 과 (3+6-a) : b = 9 : 10 두 비례식이 성립합니다. 각각의 비례식을 정리하면 5a+2b=30, 10a+9b=90 이 나옵니다. 연립방정식을 풀면 각각 b=6, a=3.6(18/5) 이렇게 나오고, 따라서 넓이인 5a+3b=36 입니다. 그런데 초등 5학년 문제니 연립방정식 안 세우고 푸는 방법이 있지 싶은데... 그건 지금 생각이 안 나네요
16/05/17 16:22
그르브를 x라 하고 므드브를 y라고 하면 느르브는 2x 느므브는 2y,
이걸 조합해서 그느므와 느드르의 면적에 대입하면 x=y=9 느므브르=2x+2y=36
16/05/17 16:36
초등학교면 닮음으로 푸는 게 좋지 않을까 싶네요. 우선 10:5와 6:3이 같음을 이해한 뒤 선분 르므와 선분 그드가 평행하고 길이비가 2:3이기 때문에 사각형의 넓이는 삼각형 그느므*2/5과 느드르*2/5의 합이므로 계산하면 36입니다.
16/05/17 23:36
제가 멍청해서 이해가 안되나 봅니다... 선분 르므와 선분 그드에서 2/5가 어떻게 나오는지 혹시 설명해주시면 안될까요 ㅠㅠ 무지해서 죄송합니다...
16/05/17 23:46
네, 삼각형 브그드와 브므르가 닮음비 3:2로 닮았으므로 선분 브그와 브므, 그리고 선분 브드와 브르도 역시 3:2의 길이비를 가집니다. 따라서 삼각형 느브르의 넓이는 삼각형 느드르의 넓이의 2/(2+3), 마찬가지로 삼각형 느브므의 넓이도 삼각형 느그므의 넓이의 2/(2+3)가 되겠지요? 쓰고보니 꽤 많이 생략했네요, 히.
16/05/19 07:54
도형의 닮음은 중학교 2학년때 배우는 개념입니다.. 저 문제는 초등학교 5학년 내용일거구요. 미지수 개념은 초등학교 수학에서 ''어떤 수' 라고 표시 되는게 있어서 써도 될겁니다.
16/05/17 23:37
우선 느브에 보조선을 하나 긋고요. 그르브 면적을 a 라 하고 느드브 면적을 b 라 할 때 느르브는 2a, 느므브는 2b 가 되겠고, 따라서 그느브 넓이는 3a, 느드브 넓이는 3b 가 되겠네요. 색칠한 곳의 면적은 2a+2b=2(a+b) 이구요. 그럼, a+b 의 값만 알면 되겠고...... 일단 삼각형 그느므와 느드르의 합을 구해보면 그느므의 면적은 45, 느드르의 면적은 45니까 합치면 90. 근데 두 삼각형을 합쳤을 경우, 색칠한 부분이 두 번 들어간 셈이니 (a+b)+2*(2a+2b)=90 이네요. 풀면 5(a+b)=90, a+b=14 이므로 2(a+b)=28. 즉 색칠한 부분의 면적은 28 아닌가요?
16/05/17 23:56
아니 근데 초등학교 문제에서 미지수 쓴 기억이 없 것 같은데....
미지수 안쓰고 푸는 법을 모르겠어요 ;; 소야테님이 말씀하신 닮음이 생각이 안남 ㅠㅠ 뭐였더라 ;;
|
||||||||||||