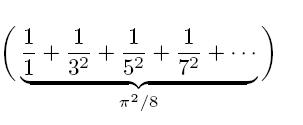|
:: 게시판
:: 이전 게시판
|
이전 질문 게시판은 새 글 쓰기를 막았습니다. [질문 게시판]을 이용바랍니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
10/04/05 21:39
퓨리에 변환으로 풀면 될거 같구요. 관계식을 세워서 적분 몇번 하시면 되는데
자세한건 아랫분이 해주실겁니다.
10/04/05 22:14
안녕하세요 드디어 이과생이 왔습니다
별로 어렵지는 않은 문제지만 지금은 곤란하니 조금만 기다려주세요 아랫분이 해주실겁니다(6)
10/04/05 22:16
오 수학문제군요! 수학/화학과 이중전공생입니다.
오일러 증명부터 시작하죠. sinx에 대해서 우선 테일러 전개합니다. sinx = x - (x^3)/3! + (x^5)/5! - (x^7)/7! ... 이걸 통째로 x로 나눠서 (sinx)/x, 이걸 f(x)라고 하죠. 즉 f(x) = 1 - (x^2)/3! + (x^4)/5! - (x^6)/7! ... 이 급수는 물론 절대수렴합니다. f(0) = 1이고, sinx는 x = 0, x = ±pi, x = ±2pi, x = ±3pi, x = ±4pi, ... 등에서 0이니까, (pi는 물론 파이, 즉 3.141592어쩌구죠) x = 0일 때 1이고, x = ±n파이를 근으로 갖는 무한 다항식으로 쓸 수 있습니다. 즉 f(x) = (1 - x/pi)(1 + x/pi)(1 - x/2pi)(1 + x/2pi) ... 이걸 항 두 개씩 묶어서 정리하면 f(x) = sinx/x = 1 - (x^2)/3! + (x^4)/5! - (x^6)/7! ... = 1 - (x^2)/(pi^2) {(1 - (x^2)/(4pi^2)} ...
등식의 오른쪽을 전개하면 f(x) = 1 - 1/(pi^2) + 1/(4pi^2) + 1/(9pi^2) + ... x^2 + (...)x^4 + ...
이걸로 계수를 비교하면 - 1/3! = - 1/(pi^2) + 1/(4pi^2) + 1/(9pi^2) + ...
pi^2을 곱해주면 이게 뜨죠. (pi^2)/6 = 1/(1^2) + 1/(2^2) + 1/(3^2) + ... (그림으로 그리면 훨씬 편할텐데; 아무튼 제곱수의 역수의 합이 파이제곱 나누기 6이 된다는 이상 오일러의 증명입니다) 여기까지 됐으면... 이제 저 등비급수의 짝수 번째 항을 노려봅시다. 짝수 번째 항은 위의 저 무한등비급수를 1/4로 나누면 얻을 수 있죠. 그걸 원래 무한등비급수에서 홀라당 빼주시면 우리가 원하는 답인 (pi^2)/8 = 1/(1^2) + 1/(3^2) + 1/(5^2)...가 나옵니다. 직접 종이에 써 가면서 풀으셔야 할 겁니다... 그리고 아직 타임오버 안됐기를 기원합니다.
10/04/05 22:29
윗분의 내용을 간단히 정리해드리자면 리만 제타 함수 zeta(2)의 값이 sum 1/k^2 = pi^2/6입니다. 이에 대한 증명은 윗분도 해주셨고, riemann zeta function 검색해보시면 다른 증명도 꽤 나올 겁니다(윗분이 해주신 증명은 위키피디아에서 Basel Problem을 검색해보시면 나옵니다). 그렇다면 양변에 1/4을 곱하면 sum 1/4k^2 = pi^2/24가 될 텐데, 이것은 sum 1/(2k)^2 즉, 1/k^2에서 k가 짝수인 경우만 나오게 되죠. 그럼 zeta(2)에서 sum(k=짝수) 1/(k)^2를 빼주시면 게임 끝입니다.
10/04/05 22:37
나이가 들어서 산수 계산이라던지 돈 계산이 안된다고 하는 질문인 줄 알았는데. 허허..
위에 잘 나와있는데로, 1+1/2^2+1/3^2... 에서 짝수 항 빼면 간단하게 나옵니다.
|
||||||||||||