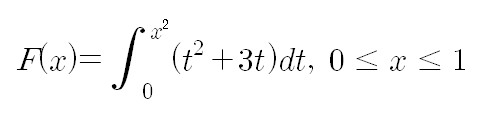|
:: 게시판
:: 이전 게시판
|
이전 질문 게시판은 새 글 쓰기를 막았습니다. [질문 게시판]을 이용바랍니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
08/12/10 21:43
g(t)=t^2+3t, G(t)=∫g(t)dt 라 두면
F(x)=G(x^2)-G(0) 따라서 F'(x)=G'(x^2)*(2x)=(x^4+3x^2)(2x)=2x^5+6x^3 가 되겠습니다.
08/12/10 21:48
t 에 대해서 부정적분해서 원시함수를 구한후에 상한을 x^2 하한을 0으로 대입하면 됩니다. 적분구간이 미지수라고 해서 특별하게
생각할건 없어요.
08/12/10 21:53
비상 / 이재열님 /// 답변 정말정말 고맙습니다.
제가 지금 헷갈리는게 x가 범위가 지정되있다는 사실입니다... 그래도 상한 하한 대입하여 빼기해주면 답을 구하게 되는건가요?
08/12/11 00:04
적분하여 x^2 과 0 을 대입하면 F(x)를 구할수 있는데 저기서 0=<x=<1 이라는건 0~1에서만 F(x) 가 저 식을 만족한단 뜻이지요.
즉, 0~1의 범위에서만 주어진 식을 만족한다는 뜻입니다. F'(x)도 마찬가지구요.
|
||||||||||||