|
:: 게시판
:: 이전 게시판
|
이전 질문 게시판은 새 글 쓰기를 막았습니다. [질문 게시판]을 이용바랍니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
11/05/12 13:18
indeteminate problem이니 strain을 고려해서 풀어야죠. 정역학만으로는 안됩니다.
합력에 관한 식 하나, 위치에 관한 식 하나 해서 힘과 strain을 구할 수 있습니다.
11/05/12 14:03
문제그대로에요 글자하나안틀리게 적은거에요
그리고 그렇게 푸는건 아는데 식을 어떻게세워야할지를 물은건데 그렇게 뭉뚱그려답하시면....
11/05/12 17:18
Level 9 님의 말씀대로 델타 = PL/EA 과 시그마F=0 으로 풀립니다.
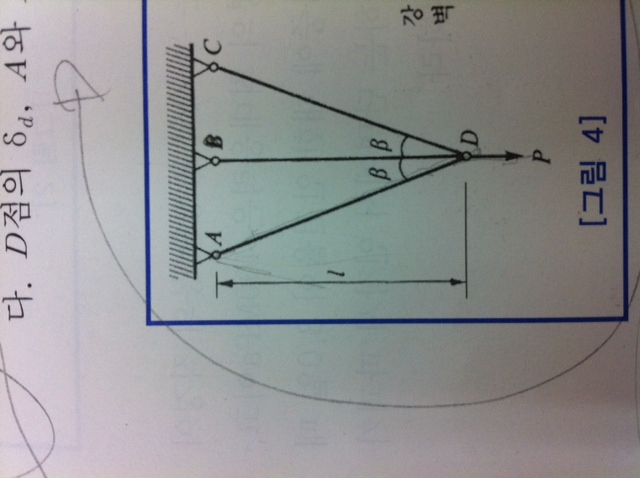
가운데 봉에 작용하는 힘을 A, 좌우 대각선 봉에 작용하는 힘을 B라고 두겠습니다. 시그마 F = 0 에서 A+2B*cos(베타)=P 또한,d_A = Al / EA d_B = B* l / cos(베타) / EA 입니다.
여기서,,, 늘어나기 전과 늘어난 후의 그림을 그려보시면 베타+d(베타)(작은 직각삼각형) 와 베타(큰 직각삼각형) 를 꼭지로 하는 직각 삼각형 2개가 나오는데요, 큰 직각삼각형에서 작은 직각삼각형을 뺀 둔각 삼각형에 대해서 코사인 제 2법 칙을 쓰시면 다음과 같은 식을 얻으실 수 있습니다. ( 길이가 가장 긴 변의 길이 : l / cos(베타) + d_B, , 나머지 두 변의 길이 : d_A, l / cos(베타) ) l / cos(베타) + d_B ^2 = (d_A)^2 - 2*d_A*ㅣ / cos(베타) *cos(PI - 베타) + ㅣ / cos(베타) ^2
여기서 (d_B)^2 과 (d_A)^2 은 미소길이의 제곱이므로 무시하면, 최종적으로 d_A = d_B / cos (베타) (주의 : d_A = d_B * cos (베타) 가 아님) 라는 식을 얻을 수 있습니다. 이제 이를 d_A = Al / EA d_B = B* l / cos(베타) / EA 에 대입하시면
d_A = Al / EA = B* l / cos^2(베타) / EA 가 됩니다.
위 식에서부터 A = B / cos^2(베타) 가 됩니다. 이제 이를 시그마F=0 에 대입하면, A ( 1 + 2*cos^3(베타) ) = P 를 얻을 수 있고, 여기서 A = P/(1+2cos^3(베타)) B = P*cos^2(베타)/(1+2cos^3(베타)) 를 얻을 수 있습니다.
|
||||||||||||