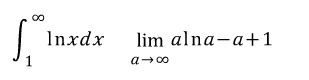|
:: 게시판
:: 이전 게시판
|
이전 질문 게시판은 새 글 쓰기를 막았습니다. [질문 게시판]을 이용바랍니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
09/09/28 15:51
일단 이 적분은 무한대라서 구할 수가 없겠네요
a가 e보다 크면 항상 alna가 a보다 빨리 커지니.. 그래프 그려보면 쉽게 알 수 있을 거에요.
09/09/28 16:32
lnx 의 극한값이 무한대이므로 발산은 확실합니다. 무한대의 함수가 적분값이 있으려면 반드시 해당 함수의 극한값이 0 이어야 하지요.
limf(x) 가 0 이 아니면 시그마f(x) 가 발산하는 거라고 생각하시면 되요. 다만 저도 오래되서 풀이법은 기억이...
09/09/28 16:59
대충 풀이법 끄적여봅니다..;;
극한을 비교하는 방법을 사용하려고 합니다. 즉, 작은게 발산하면 큰것도 발산한다는 정리를 쓰는것이죠. alna - a + 1 > alna - a = lna^a - lne^a = ln(a/e)^a a/e = t 로 치환해봅시다. 그러면 ln(t)^et 가 되겠죠. 다시 극한을 비교하는 방법을 사용해서... ln(t)^et > ln(t)^t > ln(t) 이므로 ln(t)는 t가 무한대로 갈때 발산하므로 원래 극한값 또한 발산합니다.
09/09/28 17:12
아스트랄님 말씀이 가장 수학 문제 푸는데 도움이 되는 '개념'인 것 같네요.. 모든 문제를 식으로 풀어내서 답을 구해야 할 필요가
없습니다. 적분이라는 것은 면적인데 lnx처럼 증가하는 함수에 1부터 무한대까지 적분을 하면 당연히,, 무한대가 나오죠. 그리고 극한값을 따질때는 차원이라고 해야할까, 크기라고 해야할까 모르겠지만.. 같은 차원에서 비교가 되는 대상끼리 비교만 해주면 됩니다. 예를 들면 lnx < 루트 x < x < x^2 < x^3 <........................< x ^10000 < 2^x 이런것처럼요. 위의 것들은 계수와 상관없이 같이 무한대로 간다고 했을때 순서대로 '비교'도 안되는 대상들입니다. 따라서, 뒤쪽식은 고민할 필요가 없는게 x에 lnx를 곱한것이 뒤쪽의 x보다 더 높은 차원의 것이므로 뒤의 x앞에 10000이 붙어있다 치더라도 비교가 안되는 대상입니다. 당연히 무한대입니다..(뭐 굳이 풀이법을 식전개로 만들려면 만들 수는 있겠으나 고등과정이라면,, 이정도로만 이해하는 것이 문제푸는데 훨씬 좋을거라 확신합니다.)
|
||||||||||||