|
:: 게시판
:: 이전 게시판
|
이전 질문 게시판은 새 글 쓰기를 막았습니다. [질문 게시판]을 이용바랍니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
09/01/18 19:50
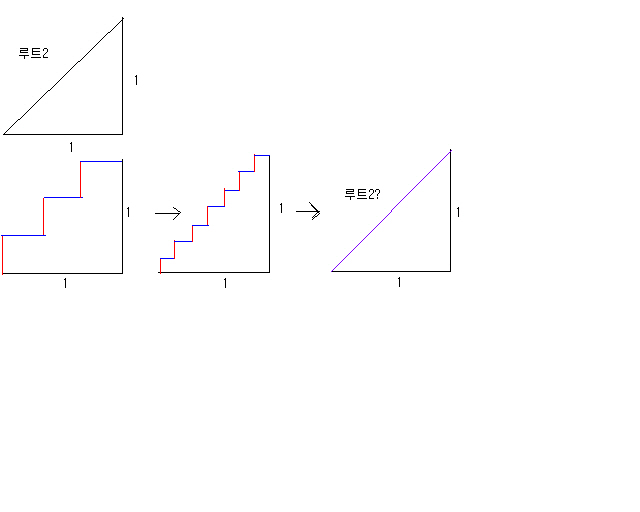
Hildebrandt님// 원도 다각형이 무수히 각이 많아지면 원이 되는거 아닌가요? 원넓이랑 원주 구하는것도 그 원리로 구하는데...
09/01/18 20:04
물론 겉보기에는 계속 세분화하다보면 직각삼각형과 똑같은 모양으로 보이겠죠..(무한개로 세분화되면)
하지만 실제로 저 도형은 직각삼각형이 되지 않습니다. 글쓴분 말처럼 길이가 2가 되기 때문이죠.. Incognito님이 하신 방법은 결국 (1을 무한개 쪼갠것들의 전체합 + 1을 무한개 쪼갠것들의 전체합) 이므로 값이 2가 되는것입니다..
09/01/18 20:05
10년전쯤에 수학선생님이 저희에게 질문했던 것과 같은 문제군요.
기억이 맞다면 아마 답은 무한(혹은 극한)은 현실이 아니다, 였던 것 같습니다. 본문에 무한히 세분화하면 결국 직각삼각형의 모양이 나온다고 하셨는데 이는 반대로 유한의 단계에서 정밀하게 관찰하면 '직각삼각형'의 모양에 가까운 계단형일 수 밖에 없습니다. 또 직각삼각형의 모양이 되었다 한들 그것은 그렇게 보이는 것이지 실제로 그러하지 않다, 라는 것 역시 알고 있는 사실이구요. 다른 예를 들어보면 1과 1-x, 두 값을 비교하면 차이는 x가 0보다 크다는 전제하에 1이 무조건 큽니다. 그러나 극한개념에서 x가 +0에 수렴하면 두 값이 같다고 할 수 있죠. 하지만, 현실에서는 그것이 성립되지 않습니다. x가 +0에 가까워진다 하더라도 '무한'이 아닌 단계에서는 0보다 클 수 밖에 없으니까요.
09/01/18 20:10
한가지 더 얘기하자면 글쓴분이 한 방법으로 한 도형의 넓이와 기존의 직각삼각형의 넓이는 같게 됩니다..
극한의 원리에 의해서 같아진다고 생각하면 됩니다 ^^
09/01/19 04:51
극한에서는 약간의 차이가 별 의미없지 않나요. 1억미터하고 1억1미터하고는 숫자상 다르지만, 아마 멀리 태양쯤에서 보면 똑같을수도...
즉, 1.4142나 2나 극한으로 보내면 비슷한 맥락이 되려나요.
|
||||||||||||