|
:: 게시판
:: 이전 게시판
|
이전 질문 게시판은 새 글 쓰기를 막았습니다. [질문 게시판]을 이용바랍니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
08/09/30 01:51
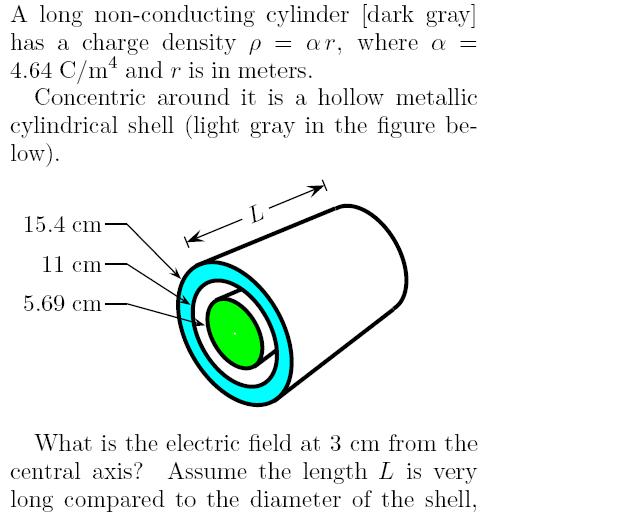
charge density의 단위가 좀 이상하네요. 어떻게 분모가 m^4가 될 수 있는 건지..
식에서 오른쪽 부분이 잘못 된 것 같네요. 구형이 아닌데 (파이)*r^3으로 charge를 구하는건 아닌거 같네요.
08/09/30 01:53
아아아악ㅠ 이놈의 영어 울렁증이 절 가로 막네요T^T
문제 해석 좀 누가 해주시면 어떻게 손 써볼 수 있을꺼 같긴한데...
08/09/30 01:59
졍님//
ρ 값이 부피당 전하의 밀도를 나타 내는 것이라면 α*r 값이 들어가니 계산적으로는 문제 없어 보이는데요? α = [C/m^4] 이고 r = [m] 니까 계산하면 α*r = [C/m^3]. 이렇게 단위가 되니까 계산상으로는 문제가 없어 보입니다. 근데 제가 영어가 약해서 문제 자체가 무슨 뜻인지를 몰라 α 값의 의미가 뭔지는 아예 모르겠네요. 문제라도 알면 의미가 맞는지 아닌지 정도 파악 가능할텐데.T^T
08/09/30 03:31
buffon님//
일단 정확하진 않지만 아는 한도내에서 문제해석하고 풀어보았습니다. 글로 적으려니 복잡하네요. 읽기 힘들어도 좀 이해해주세요. [ ]는 단위 표시입니다. 저기 적힌 숫자가 각 원의 지름이라고 가정하고 풀었습니다.(아니면 저 울겁니다.T^T) 그리고 중심의 축에서 3cm 떨어진 곳의 전기장을 구하는 것이 문제이기 때문에 가우스 법칙을 사용합니다. (축에서 3cm 떨어졌다는 뜻은 하늘색 부분과 연두색 부분의 사이에 위치하게 됩니다. 반지름이 3cm, 즉 지름이 6cm이므로) ε0 * Φ = q 라는 식을 이용합니다. 위에 나온 ρ의 값이 α*r의 값이랑 같구요. α은 4.64 [C/m^4]. (α값의 의미는 정확히 모르겠습니다.) 일단 전하량을 알기 위해 ρ값을 이용합니다. 제가 해석한 ρ값은 단위 부피당 전하량이기 때문에 바깥부분(하늘색)의 부피와 안부분(연두색)의 부피를 구합니다. 바깥부분의 부피 : {(7.7 [cm])^2 - (5.5 [cm])^2) * 파이 * L 안부분의 부피 : (2.845 [cm])^2 * 파이 * L 이렇게 부피를 구한 각각에 ρ를 곱해주게 되면 각각의 부피에 대한 전하량이 나오게 됩니다. 그리고 ρ값과 α*r값이 같기 때문에 대입할 수 있습니다. 바깥부분의 전하량 : {(7.7 [cm])^2 - (5.5 [cm])^2) * 파이 * L * ρ = {(7.7 [cm])^2 - (5.5 [cm])^2) * 파이 * L * α * r 안부분의 전하량 : (2.845 [cm])^2 * 파이 * L * ρ = (2.845 [cm])^2 * 파이 * L * α * r 이렇게 전하량을 구한다음에 ε0 * Φ = q 을 이용합니다 ε0 * Φ = q ε0 * ( ∮ E · dA ) = q 여기서 전기장의 세기는 전하의 밀도가 일정하므로 변화가 없습니다. 그리고 면적도 변화가 없고 일정한 값을 가지게 됩니다. 그래서 아래와 같은 식이 가능하게 됩니다. ε0 * ( E * 2파이 * r * L ) = q E(전기장) 에 대해서 정리하면 E = q / ( 2파이 * ε0 * r * L ) 이렇게 됩니다. 이제 전기장에 대해서 정리를 했으니 위에서 구한 전하량의 값을 대입한 다음 바깥쪽(하늘색)과 안쪽(연두색)의 전하가 같은 전하라면 전기장의 방향은 반대이기 때문에 한쪽을 + 값으로 잡고 빼주어야 됩니다. (바깥쪽의 부피가 더 크므로, 전하량도 많기 때문에 전 바깥쪽 부분에서 만들어지는 전기장의 방향을 + 방향으로 잡겠습니다.) 바깥부분의 전기장 : E(out) = {(7.7 [cm])^2 - (5.5 [cm])^2) * 파이 * L * α * r / (2파이 * ε0 * r * L ) 안부분의 전기장 : E(in) = (2.845 [cm])^2 * 파이 * L * α * r / (2파이 * ε0 * r * L ) 이제 계산을 하면, (여기서 단위를 고치고 가겠습니다. α값과 r값의 단위가 m로 되어 있기 때문에 cm를 m로 바꾸고 계산하겠습니다. 그리고 분자 분모에 같이 있는 파이, L, r 값들을 전부 약분해줍니다.) 바깥부분의 전기장 : E(out) = {(7.7 * 10^-2 [m])^2 - (5.5 * 10^-2 [m])^2) * α / 2 * ε0 = (1.45 * 10^-3 [m^2]) * α / ε0 안부분의 전기장 : E(in) = (2.845 * 10^-2 [m])^2 * α / 2 * ε0 = (4.05 * 10^-4 [m^2]) * α / ε0 이렇게 계산됩니다. 답 : - 전기장의 방향 바깥부분의 전기장의 방향 (전하가 +전하라면 중심축을 향해서, -전하라면 중심축의 반대방향으로 향해서) - 전기장의 크기 (바깥부분의 전기장과 안부분의 전기장의 차이) E = (1.05 * 10^3 [m^2] ) * α / ε0 α = 4.64 [C / m^3] ε0 = 8.85 * 10^-12 [C^2 / (N * m^2 )] 따라서 E = 5.51 * 10^8 [N/C] 입니다. 이까지 읽어주시느라 고생하셨습니다. 이게 맞길 바라면서.. 그럼 이만.^^
08/09/30 06:36
아.. 밀도가 중심에서의 거리에 대한 함수로 나타난다는 의미였군요. 그럼 'α'의 단위가 그렇게 되는게 맞겠네요.
보통 위가 같은 경우에는 표면에 전하가 집중되기 때문에 면적당 전하의 밀도로 나와야 하는데라고 생각했었네요. ^^ 그런데, 문제에 대한 해석이 전 조금 다른데요.. 문제에서 a long non-conducting cylinder(dark-gray)는 안의 연두색 cylinder를 말하는 것 같고요. 전하의 밀도는 이 cylinder내에서의 전하의 밀도를 말하고 있는 거 같네요. a hollow metallic cylindricall shell(light-gray)는 연두색 cylinder를 둘러싸고 있는 파란색 cylinder인데 metallic이라고 되어 있으니, 모든 전하는 표면에 존재하겠죠. 그리고 두개의 cylinder 사이는 특별한 언급이 없으니 진공이라고 볼 수 있겠네요. 그럼, 우선 안 cylinder의 단위 길이당 전하 양을 다음 식으로 구하면 q = integral(0 to 2.845*10^-2) α * 2 * pi * r dr
그럼, 3cm 떨어진 곳에서의 전자장의 크기는 E = 1/(ε0*2*pi*(2.845*10^-2+3*10^-2)) * q 로 구할 수 있겠죠. 바깥쪽 cylinder에 의한 전자장은 바깥쪽 cylinder 내부에서는 0이 되기 때문에 계산할 필요가 없는걸로 알고 있는데, 확실치는 않네요. ^^
08/09/30 10:03
졍님//
앗~ 전하가 표면에... 제가 그부분에 대해서 생각을 못했네요.T^T 오랜만에 건드리다보니 그냥 공식에 대입을... 졍님께서 말씀하신게 맞는것 같습니다. 아~ 난 아직 멀었구나.T^T
|
||||||||||||