|
:: 게시판
:: 이전 게시판
|
이전 질문 게시판은 새 글 쓰기를 막았습니다. [질문 게시판]을 이용바랍니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
10/04/11 15:48
저도 정확히 기억은 안납니다만 노턴과 테브난의 정리를 이용 전압원을 전류원과 저항으로 변환하면 쉽게 풀릴것같습니다.
텍스트의 노턴 테브난 변환의 원리를 응용하셔서 아웃풋의 관점에서 서킷을 바라보면 쉽게 풀릴듯 싶습니다. 그리고 직류회로의 전류의 극성은 님이 가정하신 방향으로 회로를 해석하여 방정식을 풀었을때 전류값이 양의값이 나오면 님이 가정하신 방향이 맞는 것이고 음의 값이 나오면 님이 가정하신 방향의 반대방향으로 생각하면 됍니다. 자세한것은 아랫분께서...
10/04/11 16:21
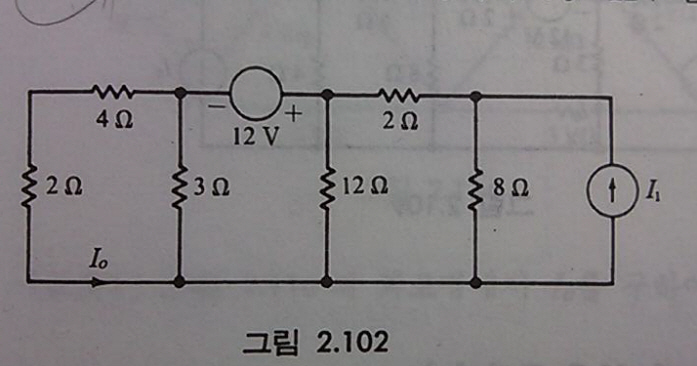
두 번째 문제 답은 13A인 것 같습니다.(연립방정식을 틀렸을 수도 있어요 계산기가 지금 없어서;;)
망루해석법? 망전류법? 파트 찾아보시면 쉽게 푸실 수 있을 것 같습니다. 그리고 부호는 수동부호규약을 익히시고 항상 고정하시면 헷갈리지 않고 푸실 수 있으실 것 같네요. 그리고 전원이 여러 개일때 푸는 방법 중 하나가 중첩의 원리 적용해서 푸는 건데요. 좀 익숙해지시면 굳이 나눠서 풀 필요가 없기는 하지만 처음에는 유용하게 쓰실 수 있을 겁니다. 책에 예제를 열심히 파고 들어보세요^^ ps. 제가 질문을 잘못이해한 것일 수도 있는데 저항은 방향과 무관한 스칼라값입니다.
10/04/11 16:32
KCL KVL 모두 전압원이나 전류원의 수와는 무관하게 적용할 수 있습니다.
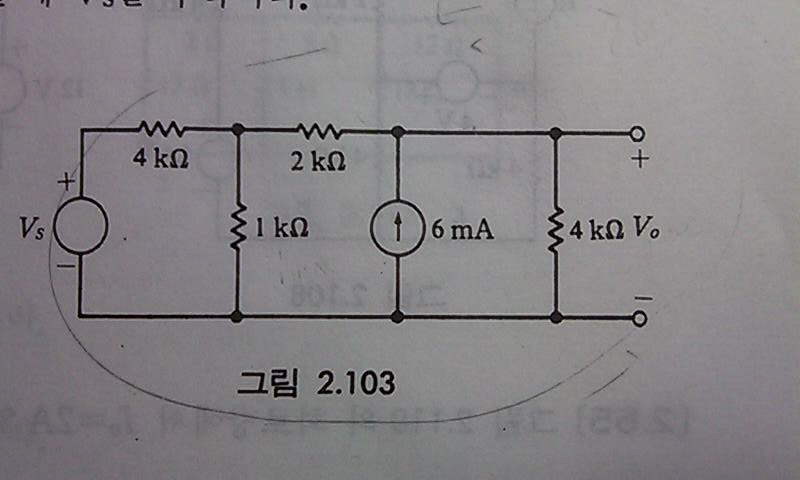
KCL은 node 방식이고 KVL은 mesh 방식이죠. KCL은 하나의 node에서 나가는(혹은 들어오는) 전류의 합은 0이다 라는 거고 KVL은 하나의 mesh(loop)에서 일어나는 전압차이(대부분 전압강하로 생각하죠)의 합은 0이다 라는 거죠. 위의 문제에서 전류원 위쪽 노드를 생각해 보면 노드 전압은 Vout일거고 그 노드에서 나가는 방향의 전류들을 생각해보면 왼쪽으로는 (Vout-Vx)/2k옴 (Vx는 그 옆 노드전압) 오른쪽으로는 (Vout-0)/4k옴 아래쪽으로는 -6mA(나가는 방향이라고 생각하면 부호가 반대겠죠?) 셋을 합하면 0이 된다는거죠. 이런식으로 식들을 세워서 연립방정식을 풀면됩니다.
|
||||||||||||||