|
:: 게시판
:: 이전 게시판
|
- PGR21 관련된 질문 및 건의는 [건의 게시판]을 이용바랍니다.
- (2013년 3월 이전) 오래된 질문글은 [이전 질문 게시판]에 있습니다. 통합 규정을 준수해 주십시오. (2015.12.25.)
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
16/04/22 23:32
두 번째 문제는 4000원, 100개네요.
xy = 40(만원) (x-0.1)*(y+50) = 45 두 식 연립하면 어느 한 변수에 대한 2차방정식이 나오는데 그 방정식의 양의 해를 찾으시면 됩니다.
16/04/22 23:34
서술형 5
x원*y개=40만원 (x원-1000원)*(Y개+50)=45만원 xy-1000y+50x-50000=45만원 40만원-1000y+50x-50000=45만원 50x-1000y=10만원 x-20y=2000 x=2000+20y (2000+20y)y=40만원 (100+y)y=20000 y제곱+100y-20000=0 (y-200)(y+100)=0 y= 200 or -100 상수여야 하기에 y= 200 xy=40만이기에 x=2000 오랫만에 수학을 했더니 체력을 다 소모했군요.
16/04/22 23:49
처음꺼는 p^2=p+1 p^4=(p+1)^2=ap+q 이런식으로 하면 이차방정식으로 나옵니다. 두번째거는 4000원 100개, 식은 윗분이 써주셨고, 세번째는 목이 안좋아서ㅠㅠ
16/04/22 23:57
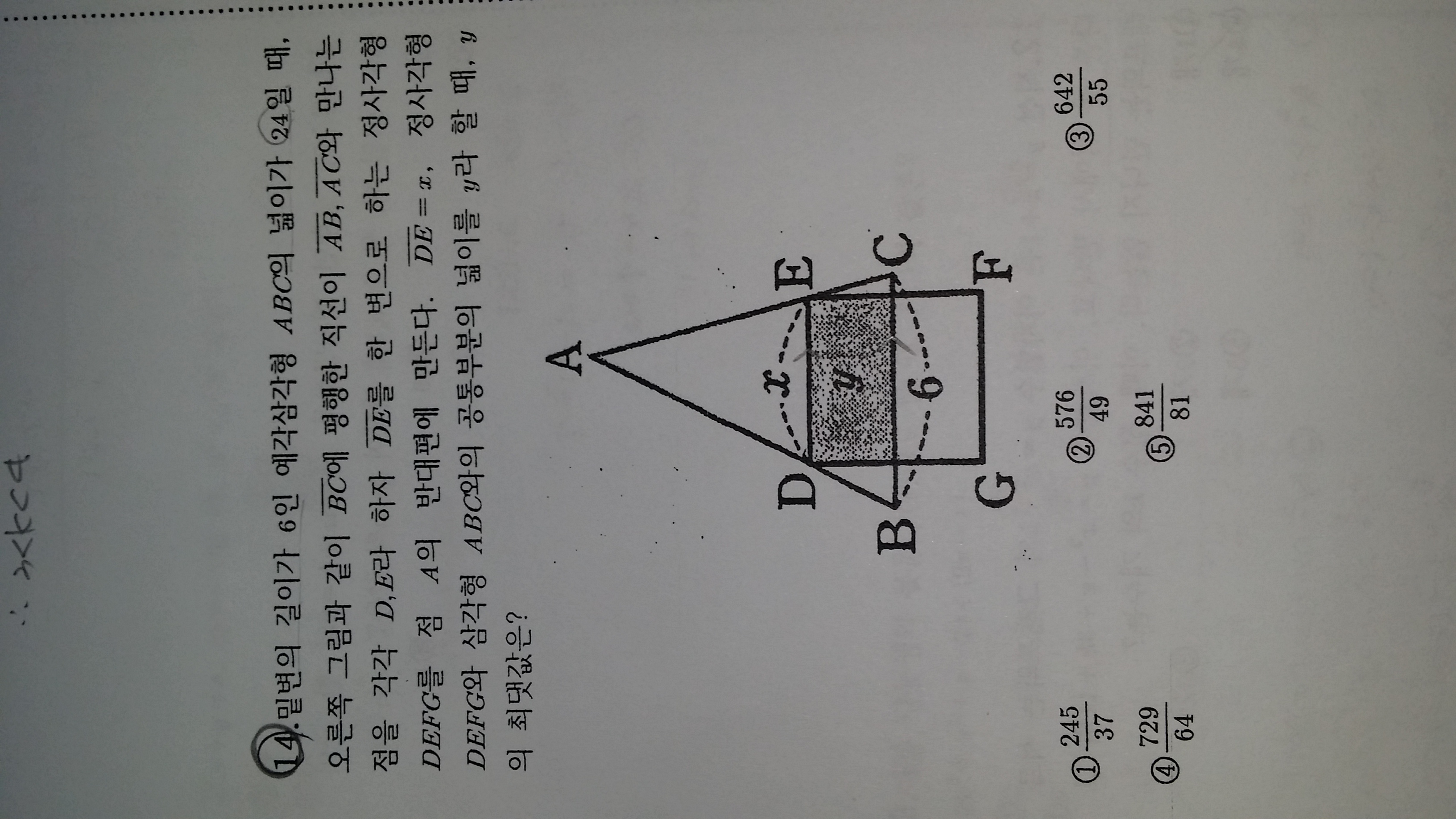
세번째 문제 풀이입니다. y와 x를 관계식을 구하는 게 급선무인데, 삼각형ABC와 삼각형 ADE가 닮음임을 이용하여 6:8=x:8-y/x 란 식을 세울 수 있습니다. 풀어서 y의 최댓값을 조사하면 x가 3일 때의 12이죠. 그런데 한 가지 문제가 있습니다. 선분DE가 어느 높이 이상으로 올라가면 정사각형이 어느 순간부터 삼각형 내부에 들어가버리는데요, 그때부턴 y=x^2이고 올라갈수록 점점 정사각형이 작아지니 선분GF가 변BC에 포함될 때가 y값이 최대라고 할 수 있겠죠. 이 때, 위와 마찬가지로 6:8=x:8-x란 식을 세우면 x=24/7이고 따라서 Max(y)=576/49입니다. 그리고 이 경우를 위해 x의 구간에 따라 함수를 나눠서 생각해야겠죠.
[0<x=<24/7] y=x^2 [24/7<x<6] y=4/3*(-x^2+6x) 이런 그래프를 그려서 확인하심 되겠습니다.
16/04/23 00:09
첫 문제는 이렇게 풀 수도 있습니다.
피보나치 수열의 일반항이 Fn = (p^n - q^n) * (1/루트5)입니다. p와 q는 문제에서 주어진 그 p와 q이구요. 두 식을 빼면, a(p^16 - q^16) + b(p^17 - q^17) = 0이 나옵니다. 그래서 a*F16 + b*F17 = 0. F16 = 987이고 F17 = 1597이므로 987a + 1597b = 0. 이게 1번. 그 다음에 p^2 = p+1을 쭉쭉 전개하면 p^16 = 987p + 610, p^17 = 1597p + 987이 나옵니다. 하다 보면 p^n = Fn * p + (F(n-1)) 이 나옴을 손쉽게 알 수 있습니다. 이걸 이용하면 (987a + 1597b)p + 610a + 987b = -1이 됩니다. 1번을 여기에 대입하면 610a + 987b = -1이 됩니다. 1번을 b에 대해 풀고 변형하면 ((1597 * 610) - (987)^2) * a = 1597이 되는데, 피보나치 수열 중에서 또 중요한 특성이 하나 있습니다. F(n-1) * F(n+1) - (Fn)^2 = -1이라는 거죠. 그래서 자동으로 -a = 1597이 되어 a = -1597, b = 987이 됩니다. 일일이 계산해도 되긴 합니다만 시간이 너무 오래 걸릴 게 뻔하니... 물론 시험문제에서는 피보나치 수열에 대한 성질을 추가로 증명하셔야 할 겁니다. https://proofwiki.org/wiki/Euler-Binet_Formula 여기 Induction step에서 피보나치 수열의 원항이 저렇게 나오는가에 대한 증명이 있습니다. 증명 중에 오타가 있는데 F(k+2)가 아니라 k+2번째 피보나치 수열이어야 말이 됩니다. 아니면 이 성질들을 이용해서 p와 q에 역으로 적용시켜서 식을 끌어내던가요.
16/04/23 00:24
1번은 두 식을 곱하고 더해서 연립방정식으로 푸셔도 됩니다. 그리고 본문 이미지에서 pq=-2 라고 적어두신 것 같은데 -1이예요.
두 식 곱하면 [a^2 - b^2 + ab - 1 = 0] 얻을 수 있고 두 식 더하면 [2a + b = -2207] 얻을 수 있습니다. 물론 p+q = 1, pq = -1, p^16 = 987p + 610, q^16 = 987q + 610 을 이용해야하죠.
|
||||||||||||||