|
:: 게시판
:: 이전 게시판
|
- PGR21 관련된 질문 및 건의는 [건의 게시판]을 이용바랍니다.
- (2013년 3월 이전) 오래된 질문글은 [이전 질문 게시판]에 있습니다. 통합 규정을 준수해 주십시오. (2015.12.25.)
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
17/07/22 06:51
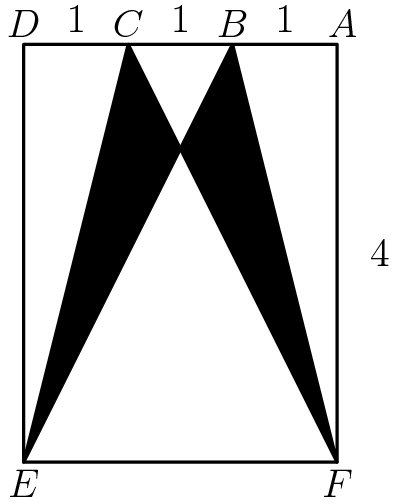
CF와 BE는 서로 대칭이니까 교점은 EF의 중점이 되죠. 이 교점을 G라 합시다.
G에서 EF에 내린 수선의 발을 G', B에서 EF에 내린 수선의 발을 B'라 하면 삼각형 BEB'와 삼각형 GEG'는 서로 닮음 관계이고 닮음비는 EB' : EG' = 2 : 1.5 = 4 : 3입니다. 따라서 BB' : GG' = 4 : 3이고, 구하는 높이는 GG' = 3입니다.
17/07/22 06:55
우선 사각형 AFED가 직사각형이겠죠? 닮음비 이용하면 됩니다.
선분 CF, BE의 교점을 G라고 하면 삼각형 GBC와 GEF가 닮음이므로 GB:GE = GC:GF = BC:EF BC:EF = 1:3이므로 높이비도 1:3, 이후는 본문에 기재하신 방법대로
17/07/22 07:06
또는 이후 이렇게 풀어도 됩니다.
△EGC와 △EGF의 공통 높이를 E에서 CF에 내린 수선으로 두면 높이가 같으므로 넓이비는 곧 밑변비가 돼서 △EGC:△EGF = GC:GF = 1:3 그런데 △EGC+△EGF = △CEF = 6이므로 △EGC = 6×(1/4) = 3/2, 같은 방법으로 △FGB = 3/2 해당 영역의 넓이 = 3/2 + 3/2 = 3
|
||||||||||||