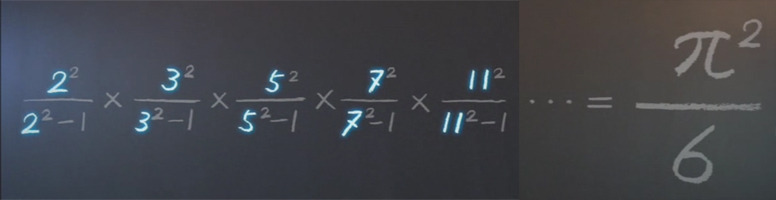|
:: 게시판
:: 이전 게시판
|
다시봐도 좋은 양질의 글들을 모아놓는 게시판입니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
13/04/06 01:22
재밌게 읽었어요. 정말 감사드립니다.
알려진 유명한 난제와 그것을 풀려고 도전하는 천재수학자들의 이야기... 제가 당사자라면 엄청난 스트레스를 받을 것 같지만, 이렇게 이야기 형식으로 듣는 것은 아주 재미있네요. 소설 <골드바흐의 추측>을 어릴 때 재밌게 본 기억도 나고 좋네요^^
13/04/06 01:32
좋은 글 잘 봤습니다.
네이버 캐스트에서 정경훈 교수님이 리만가설 관련 글들을 연재하시는 중이니, 제타함수 관심있는 이과분들은 한번 둘러보셔도 좋을 것 같습니다. 2월부터 해서 현재 4편까지 나왔습니다. 본문에 나와있는 바젤문제에 대한 내용도 다루고 있습니다. http://navercast.naver.com/contents.nhn?rid=22&contents_id=20310
13/04/06 01:36
이런 내용 너무 재밌어요.
푸엥카르의 추측을 증명해낸 페렐만은 여기엔 도전을 안하나요? 분야가 달라서 여긴 관심이 없는지? 왠지 그 사람이라면 시간만 주어진다면 10대 난제 전부를 해결가능할 것도 같은데.... 그리고 저는 전혀 문외한이고 수학의 세계를 알지 못하지만, 리만 가설도 오직 수학의 원리로만 풀기는 좀 어려울 것 같은 '황당한 추측'을 하네요. 실제 세계의 단순한 원리를 빗대어 페렐만처럼 물리법칙과 결합해서 푸는 게 더 편한 방법이 될 수도 있지 않을까요? (라고 헛된 소리를 해 봅니다) 어쨋든 이런 내용 너무 재밌어요.
13/04/06 10:56
페럴만이 푸앙카레의 추측을 풀어내는 다큐를 보고 나서 아... 페럴만 같은 사람이라면 할 수 있지 않을까? 싶었는데
쨌든 공식적으로는 안하는걸로 ㅠㅠ... 어쩌면 혼자서 고민하고 있을지도!!?
13/04/06 01:41
신기한게
물리 법칙은 창조주가 정의하기 나름이자나요 F=ma가 아니고 ma^2일 수도 있는거고 근데 숫자, 수량같은건 어떤 세계에서든 동일하게 존재할 수 밖에 없는 개념이자나요 연산이나 뭐 그런 정의가 달라져도 1,2,3,4...의 개념은 있을 수 밖에 없는거같은데 소수라는 것도 결국 필연적으로 똑같이 존재할 수 밖에 없는데 어떻게 저렇게 깔끔하게 연결이 되는건지 pi나 e가 여기서도 나오고 저기서도 나오는걸 볼때도 같은 생각을 했는데 제가 멍청한 질문을 하고있는건가요
13/04/06 01:52
저와 똑같은 생각을 하셨군요.
그런데 제 생각은 좀 달라요. F=ma^2이 될수 없다고 보네요. 왜냐면 예쁘지가 않으니까요. 직관할 수 있는 가장 단순함으로 체계를 연결한 가장 깔끔한 방법이 F=ma가 아닐까요? 물론 F=ma^2로 할수도 있을텐데 그럼.... 무슨 그림을 이렇게 더럽게 그렸니?... 내가 한수 가르쳐줄께.... 이럴 수 있지 않을까요? 신이 누군가에게 배움을 받는 건 이상한거죠. 스잡도 가장 단순한 것이 가장 아름답다고 얘기?..... (한거 맞나요?... 뭐 미니멀리즘?...) 그런데 막상 찾아보면 아주 깔끔하지 않은 부분도 많을 것 같아요. 예를 들면...... 옛날에 상상을 한 건데..... 우주를 만들때 ..... 일어버린 숫자가 있지 않을까요? 1, 2, 3, 4, 5, 6, 7, 8, 9 1과 2 사이의 거리가 3과 4사이의 거리와 동일할까요? 소름돋죠? 숫자를 그럼 왜 굳이 잃어버렸을까요?................ 그럼 체계가 더러워지니까, 일부러 잃어버린거죠. 그래도 잃어버린 것이 백그라운드에서 작용하고 있지 않을까요? 물론 상상이죠 ^^
13/04/06 15:52
조금 틀리셨습니다.
창조주가 정의할 수 있는건 원주율의 pi나 e 나 빛의 속도 c 같은 우주내의 상수들이지 F=ma는 순수 현상을 연구해서 나온 것이거든요. 우주의 기본 법칙이랑 현상학적으로 파생된 것과는 조금 달라요.
13/04/06 02:05
창조주라는 표현은 다큐멘터리에 나온 표현입니다...뭐 그냥 만약 이 세상을 신이 창조했다면 소수는 신이 남겨놓은 암호일 것이다 뭐 이런 정도의 수사학적인 표현이었는데 다큐멘터리가 창조론을 주장하는 것은 아니고 단지 재미를 위한 표현이었던 것 같습니다...
13/04/06 17:28
종교적 의미의 창조주를 지칭하는게 아니죠. 우주의 원리를 단 하나의 법칙으로 설명하려는 물리학의 최종 목적지인 "통일장"이론에 다가서는데 아주 중요한 역할을 할 것 처럼 보여서 비유적으로 쓴 것입니다. 아인슈타인이 상대성 이론을 발표해서 우주의 작동원리를 보기좋게 하나로 통합해서 설명했지만 실제로 왜 그렇게 작동하는지에 대해서는 인류 탄생 이래 한 발도 진전이 없죠. 리만 가설도 그럴 것입니다. 다만 수의 "원자"라 불리는 소수에 기본적인 법칙이 존재한다는 것과 그 법칙을 근간으로 물리 세계가 작동한다는 것을 밝혀낸다면 통일장 이론에 한 걸음 다가갈 수 있는건 자명하죠. 인간이 전능한 창조주가 된다는 것은 아니지만 우주에 존재하는 모든 힘과 물질과 에너지를 아우르는 하나의 체계를 구축할 수 있다는 것에 의미가 있지 않을까 싶네요.
13/04/06 01:58
덜덜덜 와... 수학은 하나도 모르지만 재미있게 읽었어요.
진짜 모든것을 걸고 하나의 난제에 매달리는 학자들이 내심 부럽기도 합니다.
13/04/06 02:38
이런 글을 볼때마다 정말 우주를 움직이는 단 하나의 절대법칙이 정말로 존재할지도 모른다는 생각을 하게 돼요. 인류가 그 절대적인 수식을 발견하는 순간 신이 될 수 있지 않을까 싶네요.
13/04/06 03:26
리만가설이 풀리면 현재 사용중인 보안 암호체계가 무너진다는 이야기를 어디서 주어들었는데 사실인가요? 암호자체가 소수의 불규칙성을 이용한건데, 리만가설이 풀리면 소수의 규칙성이 밝혀지고 이를 이용하면 만능키 제작이 가능해진다던데 어느정도 맞는 이야기인가요? 실제로 그렇다면 풀린다면 후폭풍이 상당할 것같네요.
13/04/06 05:10
거의 사실이 아닐 겁니다. 그러한 이야기는 조금만 검색해봐도 많이 보이는데, 제대로 원리를 규명한 문서는 (해외를 포함해도) 찾을 수가 없더군요.
어떤 수학적 명제의 증명이 구성적 방법으로만 이루어지는 것은 아니기 때문에 연관이 없다고 봐도 좋을 겁니다. 리만가설을 풀면서 어떠한 엄청난 아이디어가 사용될 것이고, 우연히 그에 따른 corollary 로써 임의의 수를 소인수분해하는 알고리즘이 등장할 수도 있겠지만 그저 가능성 (그것도 매우 희박한)정도로 보입니다.
13/04/06 13:06
공개 키 암호 방식에 사용되는게 엄청나게 큰 소수라고 합니다. 인터넷, 이메일 등 여러분야에 사용되는데 인터넷 검색해보시면 쉽게 알 수있습니다.
13/04/06 16:02
엄청나게 큰 어떤 특정한 소수... 이것이 소수인지 아닌지는 컴퓨터가 계산을 해야되는데 1부터 큰수까지 차례대로 계속 나눠가며 노가다로 계산을 해야 합니다. 따라서 슈퍼컴퓨터라도 시간이 굉장히 오래걸려요. 암호를 만드는 기관에서는 이런걸 미리 계산을 해서 갖고 있는거구요. 해커가 만약 침입을 했을때 맞닥드리는 어떤 수가 소수인지 아닌지를 맞춰야 침입을 할 수 있다면, 컴퓨터로 계산을 해야되는데 이게 아주 시간이 오래걸리기 때문에 불가능하죠. 하지만 만약 소수의 비밀이 밝혀져서 이걸 한순간에 계산해 낼 수 있다면 이런 암호체계는 무너지게 된다는 말입니다.
13/04/06 17:27
1. 공개키 암호화 방식에서 암호화한 테이블을 미리 계산하는게 아닙니다. 공개키로는 암호화는 쉽게 가능하지만 복호화가 거의 불가능한 것이고, 공개키를 제시한 측에서는 비밀키를 가지고 있어서 손쉽게 복호화를 할 수 있는거죠.
2. RSA는 공개키에서 주어진 수 n이 소수가 아닙니다. 어떤 커다란 정수 n 이 두 소수 p,q의 곱일때 p와 q 혹은 오일러 함수 phi(pq) 를 알아내는 것이 핵심입니다. 3. 위에도 썼지만 리만 가설 자체는 임의 자연수의 소인수분해(factoring)를 전혀 도와주지 않습니다. 4.현재도 리만가설은 거의 참이라고 받아들여지는 상태입니다. 이게 증명된다고 해서 수학이 아닌 분야에서 어떠한 일이 일어나기는 힘들겁니다.
13/04/07 00:13
아닙니다. 공개키 방식의 암호화는 에이엘님이 말씀하신것과 같습니다.
2^2048승의 수 테이블을 가지고 암호화하는건데.. 이거를 복호화하기엔 너무 노가다가 심해서 힘든거구요.. 리만가설 자체는 이것과 전혀 상관이 없습니다(확답은 못드립니다) 다만 P=NP 문제와는 상관이 있는데, P=NP라는 가설이 성립하게 되면 어떤 특정한 방식으로 (시간이 적게걸리는 방식으로) 복호화가 가능해집니다.
13/04/06 04:26
리만 가설에 대해 잘은 모르지만, RSA같은 경우 큰 수의 소인수분해가 힘든 점에 착안해 만든 암호기 때문에 만약 리만 가설이 밝혀짐으로써 소수를 찾는 일이 좀 더 쉬워진다면 꽤 영향을 받을 수 있을 것 같아요. 근데 왠지 제가 살아있는 동안은 안 풀릴 것 같다는게..
13/04/06 08:05
좋은 글 잘 읽었습니다. 볼때마다 궁금해지는건데, 난제라고 까지 불리우는 이런 추측이나 가설, 수식들이 증명되고 풀리면 어떤 일이 생기며 그것으로 대략 무슨 일을 할 수 있지요?
13/04/06 08:26
다큐멘터리에도 나온 내용입니다만 현재 우리가 하고 있는 신용카드 결제나 온라인 쇼핑몰 결제등을 할 때 거대 소수를 사용해서 사용자 정보를 암호화해서 보낸다고 합니다...만약 소수 배열의 원칙이 알려진다면 보안에 큰 영향을 미칠 수 있다고 하고요...과학자들의 관심은 궁극적으로 자연의 비밀을 알게 되지 않을까 하고 있답니다...뭐 통일장 이론이라든가 이런 것에 결정적 계기가 될 것으로 보고 있다고 합니다...즉 한마디로 세상을 움직이는 물리 법칙을 이해하게 된다는 거지요...
13/04/06 14:04
수학계 안에서는 리만가설과 동치인(리만가설이 참이면 이러한 명제도 참이다) 수많은 명제들이 자동으로 증명되는 셈이고, 리만 가설의 참을 전제하고 논의를 진행한 이론들도 참으로 인정받게 되므로 수학계 내에서의 거대한 발전이라고 볼 수 있습니다.
수학이라는것은 자연과학에서 일종의 도구 역할을 하므로, 어떠한 사람이 발견해낸 자연법칙의 규칙성을 간단하게 표현할 수 있게 해주기도 하고(일반상대론 같은 경우), 이러한 정리 자체에서 영감을 얻어 유추가 일어날 수 있도록 도와줍니다. 정수론 같은 경우도 '이게 무슨 쓸모가 있겠어?' 하던 시절도 있었지만, 현재는 Difie-Hellman이나 RSA등등에서 정수론 분야의 지식이 핵심적으로 사용되고 있고요. 그렇지만 막상 수학자들은 이러한 정리가 증명됨으로써 뭐가 어떻게 바뀔 것인가 하는데에는 별 관심이 없는 편이죠. 미해결 문제가 있으니 풀어볼 뿐.
13/04/06 08:39
이 다큐멘타리 저도 정말 흥미롭게봤었습니다.
특히 후반부에 원자와 관련된 이야기가 나올땐 저도 모르게 '와 이거뭐야..' 했을정도니까요. 부디 제가 살아있는 동안 이 소수와 관련된 비밀이 풀리는걸 보고싶네요
13/04/06 12:12
QED 증명종료에서 남자 주인공(수학천재)이 아무리 열심히 설명해도 여자 주인공(일반인)이 그 중요성을 이해못하자 옆에서 보고 있던 친구가 한마디로 상황종료시키죠.
친구: "이거 풀면 상금 100만 달러!" 여주: "우와와와아!" 남주는 옆에서 좌절 크크크
13/04/06 14:56
뜬금없이 존 내쉬의 존내쉬운 수학 이라는 웹툰 드립이 생각납니다..;;
전혀 흥미진진하지 않을 수도 있는 소재를 아주 흥미진진하게 쓰시는 재주가 뛰어나신 듯;
13/04/07 03:13
요새 읽고 있는 책이 '수학의 밀레니엄 문제들 7' 이었는데 딱 맞아 떨어지는 글이 올라 왔네요.
사실 리만 가설이나 PvsNP 문제 정도는 일반인들이 대충 뭔지 감이라도 잡을 수가 있는데 호지 추측은 증명해야 되는 명제 자체가 어이 없더군요. '특이하지 않은(non-singular) 투사(projective) 대수 다양체(algebraic variety) 상에 있는 임의의 (특정 유형의) 조화 미분 형식(harmonic differential form)은 대수 사이클들(algebraic cycles)로 이루어진 코호몰로지 집합들(cohomology classes)의 유리 조합(rational combination)이다.' 책에 있는 문장을 그대로 옮겨 온 겁니다. 저거 읽고 바로 책 집어 던질 뻔했습니다.
13/05/11 19:09
아 완전 몰입해서 정신없이 읽었네요.
문과생도 이해할 수 있는 친절하고 재밌는 설명에 감사드립니다. 약간 소름이 돋고 무섭기까지 하네요. 흐
|
||||||||||