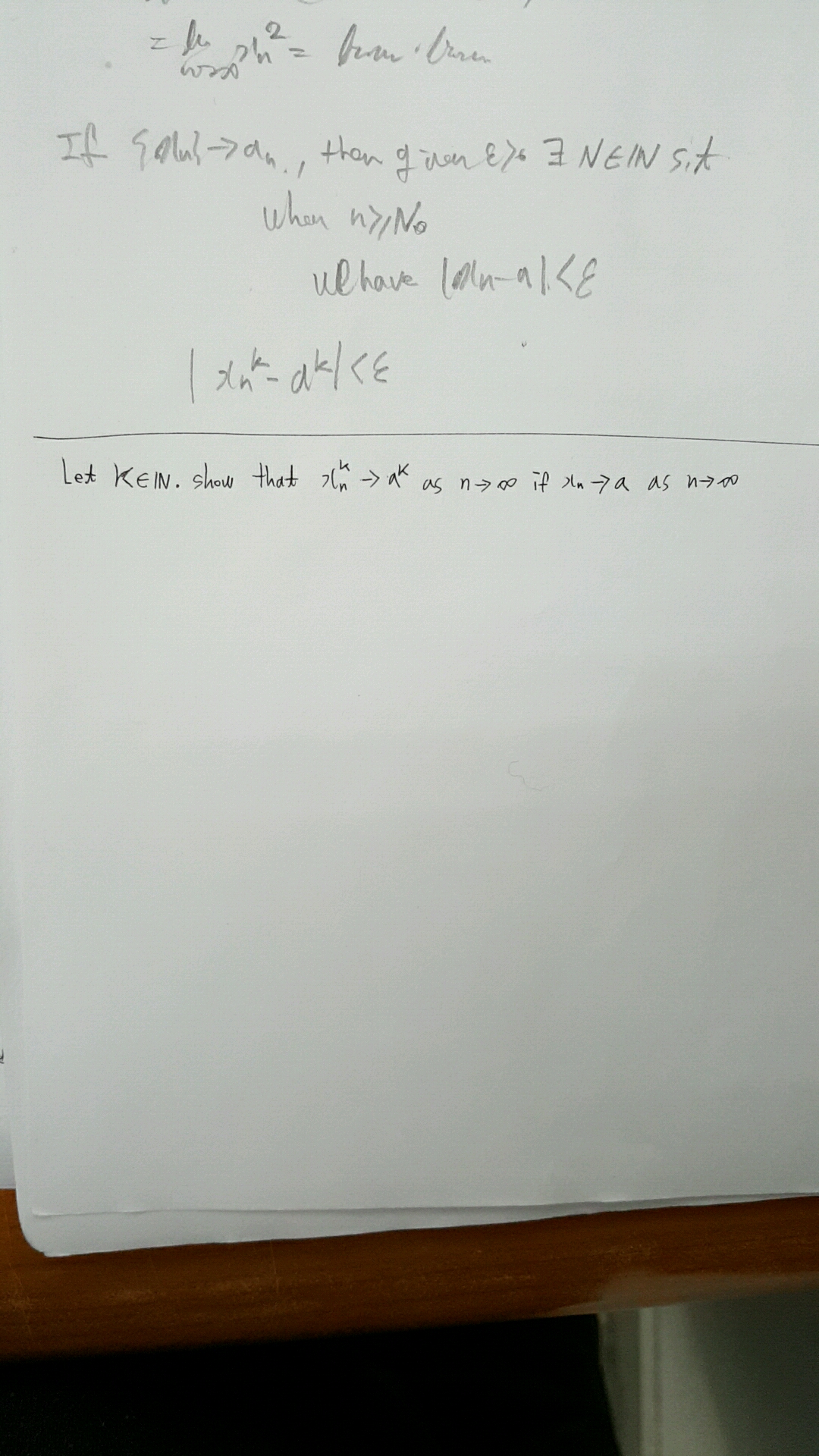|
:: 게시판
:: 이전 게시판
|
- PGR21 관련된 질문 및 건의는 [건의 게시판]을 이용바랍니다.
- (2013년 3월 이전) 오래된 질문글은 [이전 질문 게시판]에 있습니다. 통합 규정을 준수해 주십시오. (2015.12.25.)
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
17/03/21 12:35
lim(xnyn) = lim(xn) * lim(yn) 을 이용할 수 있는건가요? 가능하다면 귀납법으로 증명 되는 듯.
가정 : for some integer k, xn^i-> a^i 는 true다. let yn = xn^i. Then yn -> a^i. By using the fact above, xn*yn -> a * a^i . 다시말해 xn^(i+1) -> a^(i+1). 귀납법에 의해 모든 자연수 k 에 대해 xn^k -> a^k 은 사실이다. (가정에서 i=1 일때 사실이므로, xn^2->a^2 도 사실. 계속 이 논리를 이어나가면 모든 i에 대해 사실.) 만약 lim(xnyn) = lim(xn) * lim(yn) 을 이용할 수 없으면, 위에 해당부분만 같은 방식으로 증명하면 될 것 같네요. xn^(i+1)-a^(i+1) = xn(xn^i -a^i) + a^i(xn - a) 이렇게 해서 xn은 수렴하는 수열이므로 bounded, a^i 는 n에대해 constant 따라서 bounded, 각각 괄호는 수렴 (가정에의해).
17/03/21 13:02
lim(xnyn) = lim(xn) * lim(yn) 를 쓰지 않아도 말씀주신대로 귀납법으로 가능하군요.
저도 어쨌든 귀납법쪽으로 생각을 해본건데 교수님께서 귀납법은 거의 안쓰시고(다알지? 하면서 설명도 안하셨습니다.) 현재 진도에서는 입실론-N을 위주로 계속 수업을 진행해 오셔서 이렇게 해도 되나 하고 의구심이 들었습니다. 답변감사합니다.
17/03/21 13:46
수렴하면 유계인거랑 x^n-a^n=(x-a)(x^(n-1)+a*x^(n-2)+....+a^(n-1))인거 이용해서 귀납법 안쓰고도 가능합니다.
뭐 대충 |x|<A, |a|<A인 양수 A 잡아주면 |x^n-a^n|<=|x-a|(|x^(n-1)|+|a*x^(n-2)|+..+|a^(n-1)|)<|x-a|(n*A^(n-1)) 가 됩니다. 이정도 아이디어면 충분히 뒤에는 도출 가능하실 거에요.
17/03/21 16:18
와 감사합니다. 그렇게 인수분해 되는걸 생각도 못했네요.
그럼 squeeze 두번째 써보면 마지막항이 하나는 0이 되고 하나는 bounded니까 최종적으로 0으로 수렴하고 맨 첫항은 애초에 절대값이니까 0보다 크거나 같다고 하면 squeeze 1번으로 정리가 되겠네요. 감사합니다. 저런 인수분해 내용은 많이 풀어봐서 알고 계시는건지 직관으로 떠올리시는건지 그저 신기합니다.
17/03/26 20:26
해보는게 좋을것같은데 아직 많이 미숙한가봅니다. 막연한 두려움이 아직 없어지지않네요. 흙흙.. 다른문제들 접하면서 어떻게 접근해가는지는 지속적으로 보고 있습니다..
|
||||||||||||