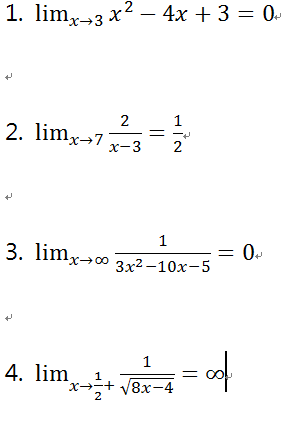|
:: 게시판
:: 이전 게시판
|
- PGR21 관련된 질문 및 건의는 [건의 게시판]을 이용바랍니다.
- (2013년 3월 이전) 오래된 질문글은 [이전 질문 게시판]에 있습니다. 통합 규정을 준수해 주십시오. (2015.12.25.)
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
20/10/28 11:37
대학교 1학년 미적분학 막 배우기 시작한 학생인 것 같네요....
고생 많습니다. 1. 과 같이 식을 쓰면 안됩니다. δ가 x에 종속되면 안될 것 같습니다. 지금 수업 들어가기 전이라 1번만 한번 해봤는데 δ=min(1, ε/3) 으로 잡으면 |x-3|<δ ≤1 이기에 -1 ≤ x-3 ≤ 1 , 1 ≤ x-1 ≤ 3, |x-1|≤ 3 |x-3|<δ ≤ ε/3 이므로 |x-1||x-3| ≤ 3 * (ε/3) = ε 입니다.
20/10/28 13:30
감사합니다. x에 따라 델타 값이 변할 수 있기 때문에 δ< ε/3 라고 함으로써 이를 해결하는 거군요.
δ= min(1,ε/3)을 잡을 줄 아는 것이 핵심인거 같네요. 완벽히 이해되진 않지만.. 감사합니다.
20/10/28 11:38
#1. 써놓으신 대로 하면 안되는 이유는, 델타에 영향을 주는 값은 입실론과 lim값을 찾는 위치(여기서는 3)만 있어야 하기 때문인데요,
써놓은 곳에는 델타가 x값에 영향을 받기 때문에 안됩니다. |x-3| < delta이면 |x-1| < 2+delta 이니까 이걸 잘 이용하시면 되겠습니다 #2. 얘는 |x-7| < epsilon * 4 * |x-3| 이 되게 delta를 찾아야 하니까 delta를 epsilon*12 와 1 둘 모두보다 작은 값으로 잡으면 될 겁니다 #3,4. 정의가 조금 달라지는 걸 아셔야 됩니다. - 임의의 epsilon에 대해 적당한 K 가 존재해서 "x > K 이면 |f(x)-L| < epsilon 이다." - 임의의 N에 대해 적당한 delta가 존재해서 "|x-a| < delta 이면 f(x) > N 이다." 정의만 아시면 K 나 delta는 대충 잡아도 대부분 따옴표 식을 만족시킵니다
20/10/28 13:57
#1은 윗분과 인내의고대장고님 덕분에 대략이해가 갑니다. 감사합니다.
이를 바탕으로 #2를 해보았는데 인내의고대장고님과 약간 다른 부분이 나온걸 보면(저는 delta = min(1,10ε)이 도출되었습니다ㅠ) 아직 한참 고민해야할 거 같습니다.
20/10/28 15:39
퇴근전에 잠깐 시간이 남아서 추가로 언급하자면
입실론 델타 기법은 극한의 수렴/발산을 주장하고자 하는 사람(A)이 누군가(B)에게 설득하는 상황이라고 이해하면 좋습니다. 예를들어 1의 결과를 주장하는 A, 반대하는 B가 있는 상황을 가정합니다. A : x의 값을 내가 원하는만큼 3에 가까이 갈 수 있다면, f(x)의 값을 얼마든지 0에 가깝게 만들수있어. B: 아닌것 같은데. f(x)와 0의 차이를 0.3보다 작게 할수있어? A: 물론이지. x와 3의 차이를 0.1보다 작게하면 가능해. B: 그럼 f(x)와 0의 차이를 0.00003보다 작게할수 있어? A: 물론이지. x와 3의 차이를 0.00001보다 작게하면 가능해. 이런식의 흐름을 생각하시면 이해하시기가 좀 수월하지 않을까 생각합니다.
|
||||||||||||