|
:: 게시판
:: 이전 게시판
|
- PGR21 관련된 질문 및 건의는 [건의 게시판]을 이용바랍니다.
- (2013년 3월 이전) 오래된 질문글은 [이전 질문 게시판]에 있습니다. 통합 규정을 준수해 주십시오. (2015.12.25.)
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
19/09/17 10:05
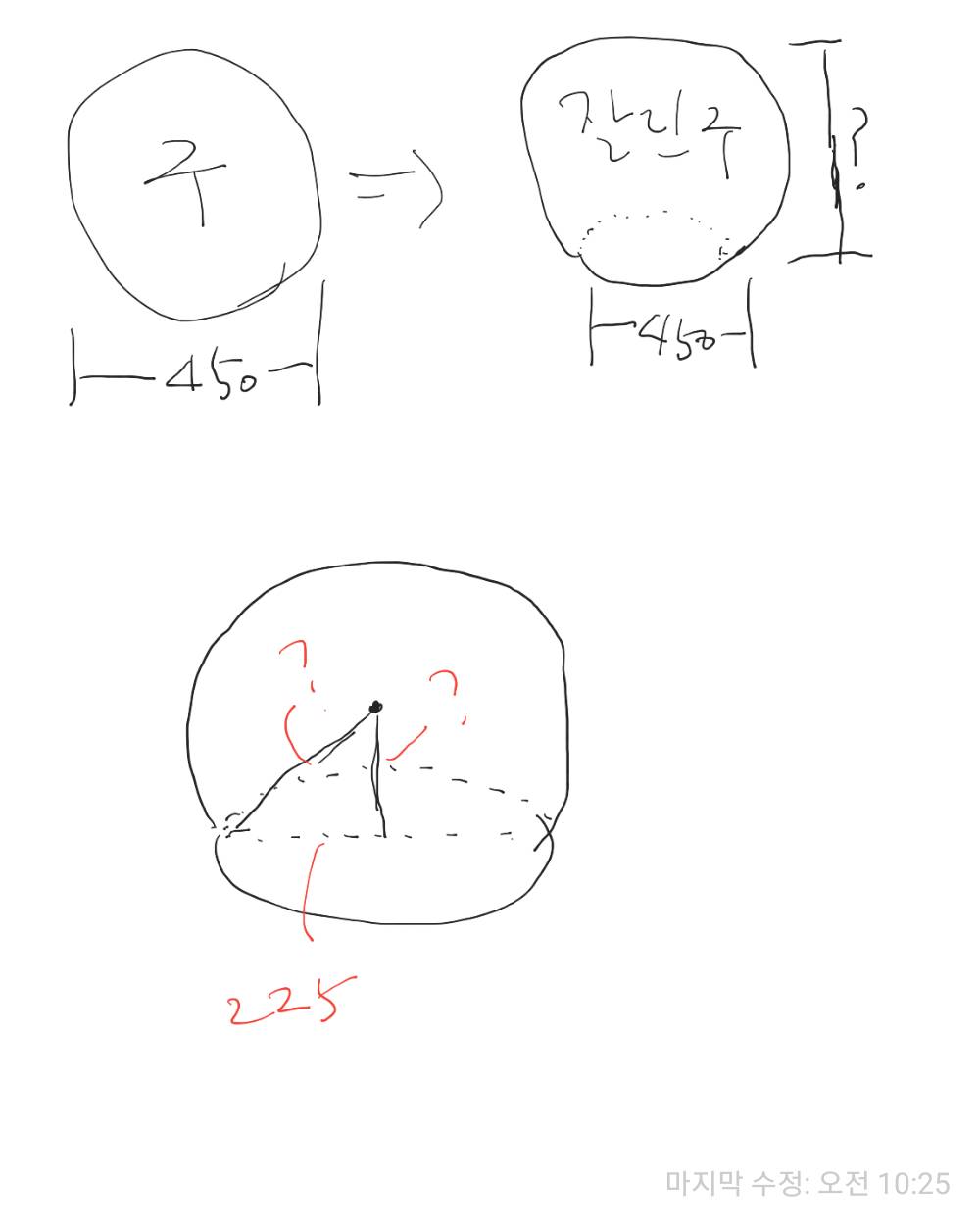
구의 반지름을 빗면으로 하는 직각삼각형을 이용하면 됩니다. 바닥원의 반지름과 구의 반지름을 가지고 피타고라스 정리를 이용하면 잘린 구의 밑면에서 구의 중심까지의 거리를 계산할 수 있습니다. 잘린 구의 높이는 여기에 구의 반지름을 더하면 되구요.
19/09/17 10:17
(수정됨) https://ko.m.wikihow.com/원의-반지름-구하기
녹은 면의 넓이 -> 원의 넓이구하는 공식에서 -> 녹은면의 반지름 을 구하시고, 구의 중심에서 녹은면까지 선을 그으면 반지름이니까 피타고라스의 정의로 구의 반지름^2 = 녹은면의 반지름^2 + [구의 중심에서 녹은면까지의 높이]^2 을 사용하면 [구의 중심에서 녹은면까지의 높이] 를 구할 수 있습니다. 구가 중심 이상 남았으면 구의 반지름 + [구의 중심에서 녹은면까지의 높이] 를 계산하면 되고, 구가 중심 이하가 남았으면 구의 반지름 - [구의 중심에서 녹은면까지의 높이] 를 계산하면 됩니다.,
19/09/17 10:46
녹기 전과 후의 형상이 정확히 구의 형상인지, 특히 녹은 후에서는 아래의 절단된 면을 제외한 부분을 제외하고 남은 부분이 정확히 구와 동일한 형상을 하는 지가 가정에 들어가야하는 게 맞겠지요?
녹기전 구의 부피 = 녹은 후의 구의 부피 이기 때문에 녹기전 부피 = 4/3 *pi*r^3 일 것이고 녹은 후에 대해서는 녹은 후의 구 형상의 반지름 r'에 대해서 4/3pi*r^3 = 4/3pi*r'^3 - (절단면처럼 생긴부피) 절단면처럼 생긴 부피 = 부분 구 (그러니까 호를 면적적분한 형태 ) - 절단면을 아래면으로 하는 원뿔 부피 로 할 수 있지 않을까 한데요.. 수식으로 될지 모르겠는데, 부분 구에서 중심입체각(혹은 중심각)과 원뿔 부피 구할 때의 높이의 관계식을 통해서 값이 나올 것 같네요.
19/09/17 10:59
단면을 적분하는게 어떨까요?
요 수식 이용해서 (출저: https://blog.naver.com/leesu52/90175964946) https://ssl.pstatic.net/images.se2/smedit/2013/6/27/hifnhsw9i2apkf.jpg 구의 부피 = 잘린구의 f(x) (동일하게 sqrt(r2-x2) 일텐데, 영역이 -r'에서 r'cos(th)까지) 에 r'sin(th) = r (r은 구의 반지름, r'은 잘린구의 반지름) 이렇게 구하면 되지 않을까요? r'cos(th)는 r'sqrt(1-sin(th)^2) 이렇게 관계식으로 유도하면 될거 같은데....
19/09/17 11:20
그래서 r'이랑 r이랑의 관계식이 sin th, cos th가 되서... 결과적으로 두 부피가 같으면,
th를 구하는 식으로 바뀌게 됩니다.... 제가 유도한게 맞는지 모르겠는데 4/3*sin(th)^3 = 2/3 + cos(th) - 1/3*cos(th)^3 이거를 구하면 th가 구해지고... 모든게 풀리게 되는데 -_- th가 안구해지네요 -_-;;;;
19/09/17 11:25
바닥면부터 잘린구중심을 r-a로 놓고 풀었더니 (뚜껑높이가a)
a에 대한 3차+-3차식이 나와서 못풀겠네요 ㅡㅡ;삼각함수 쓰는게 맞는거같은데 수학놓은지 넘오래돼서..
19/09/17 11:34
wolfram alpha에 따르면
th = 2*0.584104 radian이 되어, 높이 = r'(1+cos(th)) = r / sin(th) * (1+cos(th)) 가 될거라, 680.735 가 된다네요 -_- 물론 저 식이 맞는지는 잘 모르겠습니다. https://www.wolframalpha.com/input/?i=4*%28sinx%29%5E3+%3D+2%2B3*cosx-%28cosx%29%5E3 https://www.wolframalpha.com/input/?i=450%2Fsin%282+*0.584104+%29*%281%2Bcos%282+*0.584104+%29%29
19/09/17 11:15
구가 잘린 구가 되었는데 잘린 단면의 지름이 원래 구의 지름이랑 같다구요?...
구가 맞기는 한가요?.... 녹아서 모양이 변형된 게 아니라면 구의 지름은 변경되지 않고, 잘린 단면(원) 의 지름을 새로 재셔야 하는 거 아닌가요??..
19/09/17 11:16
그림대로 잘린구의 단면의 지름이 똑같이 450 이면 잘린구가 더 커졌거나 혹은 구의 일부가 아니라 질퍼기처럼 바닥에 퍼진 형태여야 할 것 같은데요...
19/09/17 11:32
네 구가 잘린구가 되는거고 부피는 같고 잘린구의 단면 넓이와 원래구 부피를 아는상황입니다
적분해서 푸는게 맞는데 미지수가 두개라 안풀리네요
19/09/17 11:35
저라면 회전체 적분으로 구해보겠습니다.
원래 구 부피 = 인테그랄 (새구반지름^2- x^2)dx - 를 -(sqrt(r^2 - 원래구반지름^2)) 에서 r 까지 보내겠습니다.
19/09/17 11:15
짧은 생각일지는 모르겠는데 상황을 완전히 구체화 하지 않는 이상 못 구할것 같은데요.
녹은 상태에서 바닥에 떨어진다면, 금속이 몇도인지, 그 온도에서 금속의 연신율이나 점성이 어떤지, 비중량은 얼마인지, 떨어지는 높이는 얼마인지? 등등 붙은 상태에서 녹는다면 거기에 열원이 바닥인지 구를 감싼 전체인지 같은 요소들이 더 추가되야할것 같아요.
19/09/17 11:18
그리고 녹아서 붙을 정도의 온도랑 충격이면 구가 아니라 찌부러진 구가 될거라서
잘리지 않은 윗쪽 반구쪽만 보면 바닥과 평행한쪽 지름은 더 커지고 높이쪽은 작아질겁니다..?
19/09/17 11:47
잘린 상태에서 모양은 변했는데 그 모양이 완전한 구라는 말씀이신가요?
잘린 부분이 손실이 되었다면 발생할 수 없는 현상이겠고 잘린 것이 아니라 모양의 부피는 일정하면서 잘린 것처럼 모양이 변형 되었다면 부피가 같다는 것에서 변형된 구의 반지름을 구하는 방법을 알아내야 겠네요.
19/09/17 11:44
(수정됨) 음 잘린구에 반지름을 a라 두고 잘린구의 아랫부분은 y=루트(a^2-x^2)식을 0부터 b(잘린단면 반지름)까지 적분해서 구하고 윗부분은 a를 반지름으로 하는 반구니까 계산하면 a의 3차방정식이 나와서 a 구하고 높이는 a 더하기 루트(a^2-b^2)라고 계산하면 되지 않을까요?
이거 댓글로 설명하려니까 어렵군요
19/09/17 11:50
(수정됨) 원(r^2-x^2)을 -r부터 r-x까지 적분한게 225^2와 같다고 놓고 풀고
피타고라스 225^2 + (r-x) = r^2으로 r에대한 x를 풀어서 (x는 작은뚜껑 높이) 울프럼에 넣으니까 결과가 363정도로 계산이 되네요.. 3차+ -3차식 구성이라 손으로는 못푸는 문제인걸로..
19/09/17 18:21
https://www.wolframalpha.com/input/?i=x%5E2+-+y%5E2+%3D+225%5E2+and+4*%28225%29%5E3+%3D+2*x%5E3+%2B+y%283x%5E2+-+y%5E2%29
x는 변형 후 구의 반지름, x+y는 변형 후 찌그러져있는 총 높이입니다. 찌르러져있는 단면의 지름이 450이면 반지름이 225니까 x^2 - y^2 = 225^2 이 돼서 왼쪽 식이 나오고, 반지름이 x인 구를 높이를 -x 부터 y까지 넓이 적분하면 나오는 결과가 pi*((2/3)*x^3 + x^2y - (1/3)*y^3) 이 나오는데 이게 (4/3)*pi*(225)^3 이랑 똑같다고 두고 공통계수 약분한게 4*(225)^3 = 2*x^3 + y(3x^2 - y^2) 입니다. 이렇게 두고 계산기한테 풀라고 시킨 다음에 x+y 하면 대충 320.368 정도가 나오겠네요.
|
||||||||||||