|
:: 게시판
:: 이전 게시판
|
- 모두가 건전하게 즐길 수 있는 유머글을 올려주세요.
- 유게에서는 정치/종교 관련 등 논란성 글 및 개인 비방은 금지되어 있습니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
24/04/15 09:36
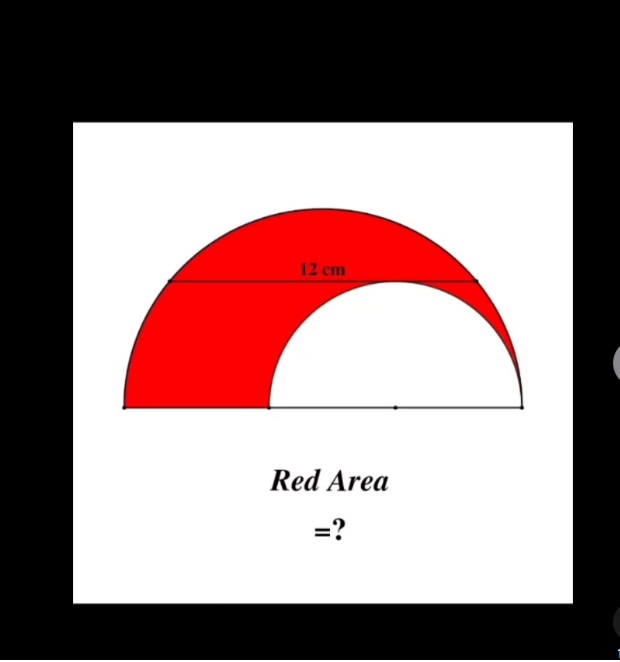
(수정됨) 22.5파이인가요?
안 맞아 떨어지는게 찝찝하긴 한데 정삼각형 하나 찾고 피타고라스 정리 이용하면 되는 것 같기두 하구요. 틀렸군요. 선분끼리 안만나는 것을..
24/04/15 09:37
작은원 반지름이 r이라 하고 큰 원 반지름이 R이라고 하면 r^2+36=R^2이고
구해야 하는 넓이는 pi*(R^2-r^2)/2 니까 18pi cm2아닌가요? 이게 아니라고...?
24/04/15 09:40
다른 조건없이 12cm 만 주어진거면, 12cm 선이 반원 위아래 어느 위치에 있든 값이 같다는 의미이고, 극단적으로 색칠한 큰반원 지름이 12cm에 빈공간 반원 반지름이 0cm일때 넓이와 같다고 하면 (12/2)^2*(1/2)*pi = 18pi 이렇게 풀었습니다. 실제 풀이과정이 궁금하네요
24/04/15 09:55
오 그러네요
큰원 반지름 R과 작은원 반지름 r의 비율과 무관하게 R2 - r2 = 36 이니까 붉은 부분 넓이는 0.5pi(R2 - r2) 이니 고정이네요. 2R = 3r이라는 조건이 불필요했군여
24/04/15 09:59
큰 원의 반지름을 R, 작은 원의 반지름을 r이라고 한다면 큰 반원의 넓이에서 작은 반원의 넓이를 뺀 면적은 1/2 * pi(R^2 - r^2) 가 되네요.
여기서 12cm 선분을 밑변으로 한 대각변의 길이가 R인 이등변 삼각형을 하나 만들 수 있고 이를 반으로 자르면 피타고라스 정리에 의해 R^2 = 6^2 + r^2 가 성립이 되네요. 즉 R^2 - r^2 = 6^2 = 36 을 알 수 있기 때문에 저 위의 공식에 대입하면 1/2 * pi * 36 = 18 pi 가 되는 것으로 보입니다 :)
24/04/15 15:23
작은원과 큰원의 중심을 같게 옮기면 큰원의 반경a와 작은원의 반경b가 피타고라스정리로 a^2 - b^2 = 6^2 가 됩니다.
그러면 붉은부분의 면적이 (πa^2 - π^2) / 2 이기 때문에 18π 가 되네요.
24/04/15 16:28
claude.ai 에 이미지 업로드 하라고 풀라고 시켰습니다. PARANDAL 님 풀이 그대로 그냥 12cm 짜리 반원으로 풀어버리네요.
To solve this problem, we need to find the area of the red semi-circular region. The formula for the area of a semi-circle is: Area = (π * r^2) / 2 Where r is the radius of the semi-circle. Given information: The diameter of the semi-circle is 12 cm. To find the radius (r), we divide the diameter by 2: r = 12 cm / 2 = 6 cm Substituting the radius in the area formula: Area = (π * (6 cm)^2) / 2 = (π * 36 cm^2) / 2 = 36π cm^2 / 2 = 18π cm^2
|
||||||||||||||