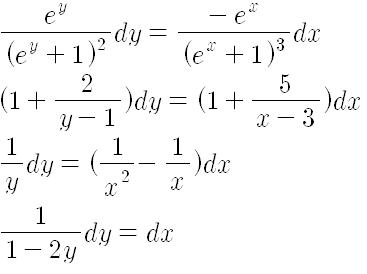|
:: 게시판
:: 이전 게시판
|
이전 질문 게시판은 새 글 쓰기를 막았습니다. [질문 게시판]을 이용바랍니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
10/04/10 23:09
첫번째 우변을 예로 들면 분모의 ex+1 을 f(x)라고 하고, f'(x)=ex 가 되므로
-f'(x) * f(x)^-3 dx 가 되죠. x^n을 적분하면 1/n+1 * x^(n+1)이 되므로 적분하면 1/2 * f(x)^-2 가 되겠네요. 적분을 키보드로 일일히 해설하려면 어지간한 중노동이라.... 다행히 문제를 보니 복잡할 것 없는 전부 같은 형태니까 f'(x) 찾아서 치환해서 해주세요. 치환적분으로 다 풀리는 간단한 형식의 문제들입니다.
10/04/10 23:54
적분법은 f(x)를 얼마나 잘 설정하느냐가 중요하고, 또 그것은 문제를 많이 풀어봐야 요령이 잡힙니다.
분모에 차수가 2차 이상이면 간단하죠. x^-n 쪽으로 놓으면 되니까요. 첫번째 문제만 설명 드리면, e^y+1 을 Y라 놓으면, Y'= e^y가 되니까 (Y')/Y^2 꼴이 만들어집니다. 이걸 적분하면 -1/Y가 되죠. (이게 왜 이렇게 되는지 모르시면 미분, 적분의 기초를 다시 공부하심이 좋을 듯 싶습니다.) 우변도 e^x+1 = X라 놓으면 X'= e^x니까 (-X')/X^3 꼴이 만들어지면서 이걸 적분하면 1/ 2(X^2) 이 되므로
Y = 2X^2 -> e^y = 2e^x + 1 이 되는 겁니다. 2차 이상 되는 거는 아까 말씀 드렸다시피 x^n 꼴로 놓고 n이 양수일때랑 똑같이 풀면 됩니다. 1/x^2 -> x^(-2) 이므로, 적분하면 x^(-2+1)/(-2 + 1) = -x^(-1) = -1/x 가 되는 겁니다. 다만 n = -1 일때는 ln x 가 되는 식으로 외워주시면 됩니다.
|
||||||||||||