|
:: 게시판
:: 이전 게시판
|
이전 질문 게시판은 새 글 쓰기를 막았습니다. [질문 게시판]을 이용바랍니다.
통합규정 1.3 이용안내 인용"Pgr은 '명문화된 삭제규정'이 반드시 필요하지 않은 분을 환영합니다.법 없이도 사는 사람, 남에게 상처를 주지 않으면서 같이 이야기 나눌 수 있는 분이면 좋겠습니다."
13/03/30 15:40
같은 거리를 가는 거면 계산할 것도 없이 빨간 쪽이 길지 않을까요? 물론v0는 같다는 전제아래..y축 성분 속도가 더 크니 중력에의해 감속해도 떠있는 시간이 길겠죠
13/03/30 15:44
근데 그럼 파란색과 빨간 색이 다른 속도에 각도도 모른다는 건데 그럼 체공시간 자체의 계산이 불가능 할 듯 하네요. 속도를 규격화 시키지 않고 시간을 물어보는 거니 시간도 정해져 있지 않은데 무슨수로 계산이 가능할지 잘 모르겠습니다. 그리고 보통 각각의 속력이다르다면 빨간색은v1파란색은v2, 이런식으로 주는게 물리 문제의 인지상정인데, 그렇지 않은걸 보니 두물체의 기본 속력은 같을거 같네요
13/03/30 15:48
그림대로라면 당연히 빨간 포물선이 오래떠잇겟죠. 문제 풀 텍스트를 보고싶네요. 브이제로와 각도가 다 변수면 문제자체가 성립을 안하는데요
13/03/30 15:54
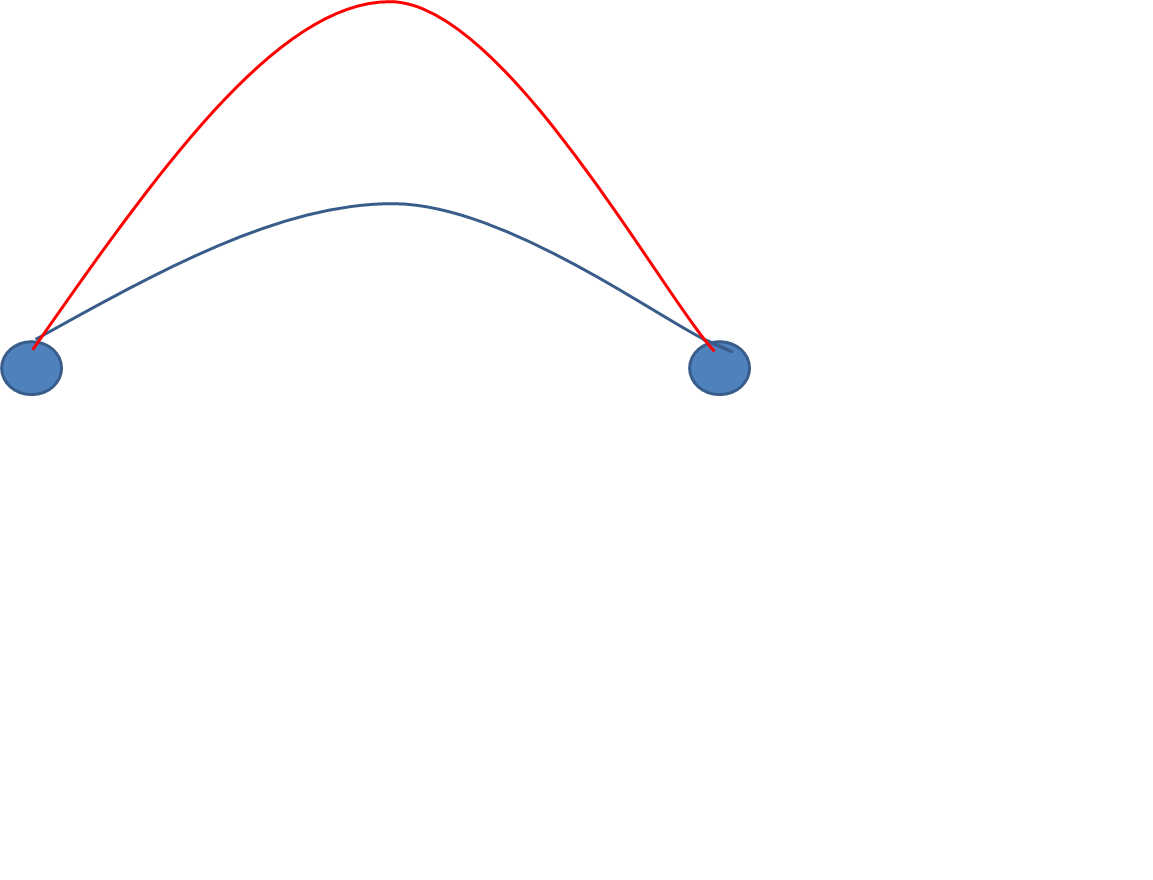
"다음 그림은 야구에서 중견수가 포수에게 던지는 다른 두궤적을 나타낸 것이다. 높고 낮은 두 궤적 중 어느 경우에 시간이 더 걸리겠는가?"
이거 달랑이고 서술하는 문제입니다...... 값을 대입하면 항상 높은각도가 시간은더 걸리게 나와요... 그런데 그걸 수학적으로 증명하기 힘든게 지금의 난관...
13/03/30 15:41
잘 맞게알고계시는데요.. 가장멀리날리려면 사십오도로 날리는거고 가장 오래체공하려면 그냥 하늘로 날리면 되죠. 이런건 상식적으로 생각하면 됩니다
13/03/30 15:41
물리는 고등학교때 물리1 이후로 안 했지만..
x축과 y축으로 운동을 분리해서 생각해 봅시다. x축의 속도나 거리가 얼마나 됐건 공이 다시 땅에 떨어지는 시간(y축 좌표가 다시 0이 되는)이 공이 도착하는 시간이죠? 그럼 x축을 아예 없다고 가정하고 그냥 위로 던진공 2개라고 생각하면 되지 않을까요. 당연히 높이 던진게 더 늦게 떨어질 겁니다.
13/03/30 15:55
그러니깐 헷갈린다는거에요 2A에 따라서 45도 기점으로 도달거리도 v0가 같으면 빨간게 길기도하고 짧아지기도하고 하거든요...
13/03/30 15:55
마찰이 없는 경우를 가정하면 도달시간은 최고점도달시간의 두 배이고, 최고점에서 속도는 0이므로 V0sinA-gt=0를 만족합니다. (t: 최고점도달시간)
따라서 2t=2V0sinA/g 니까 V0가 같다고 한다면 A가 큰 쪽이 더 긴 시간이 걸리겠네요.
13/03/30 16:05
(v1^2)*sin2A/g = (v2^2)*sin2B/g가 조건인 상황에서
2*v1*sinA/g 와 2*v2*sinB/g의 대소관계를 물어보는 문제인데v가 미지수면 구할수 없죠, 감히 절대라고 말씀 드릴 수 있겠습니다. 맨 위의 식을 더 정리하면 (v1*sinA)/(v2*sinB)=(cosB*v2))/(cosA*v1)이 되는데 이것이 1보다 크냐 작냐에 의해 결정되는 건데 v가 특정되지 않다면 불가능이죠
13/03/30 16:09
오 풀었습니다!!!!!! 간단하게 수학적으로 너무나 쉽게 증명 가능하네요! 알려드리는 것도 좋지만 그냥 한번 풀어보시라고 일단 있을게요~힌트는 sin2A = 2sinAcosA 뭐 별게 아니었군요... 머리가 굳어가네요 흐흐.. 아직 위에쓰신분들은 제가 헤맸던 과정을 답습하고 계신듯
13/03/30 16:22
네 v같지 않아도 더 간단하게 풀립니다. 추상적이지 않고 변수를 다 고려하지 않으셔도 돼요. 추가적으로 힌트드리자면 v와 sin이나 cos을 묶어서 생각하세요.
13/03/30 16:30
그리고 지적드릴게 있는데 물체의 도달거리는 v0*sin2A / g 가 아니라 v0^2*sin2A / g 입니다. 이게 오해 되셔서 결과를 도출하셨다면 다시 푸셔야 할듯 싶습니다.
13/03/30 16:30
같은 거리라면 무조건 각을 높게 던질수록 시간이 길어집니다.
(정확히 말하자면 각이 클수록 Vo가 커져야 같은 거리에 도달하거든요) 채공시간은 2Vosin@/g이고 도달거리는 Vocos@t인데 도달거리 식을 이용해 Vo을 구하면 s/cos@t이거든요. 그걸 채공 시간 t에 넣고 t에 관해서 풀면 t^2=2s*tan@/g가 나오고 tan@는 각이 클수록 커지고 t도 무조건 양수이니까 무조건 각이 클수록 시간도 길어집니다. [m]
13/03/30 16:38
이렇게 풀수도 있었군요! 와우! 근데 V0가 커져야 같은 거리에 도달한다는 말은 착각하신 것 같습니다... 큰 각도가 45도 이하일때는 오히려 V0가 작아져야 같은 거리에 도달한다는 면에서...
13/03/30 16:55
NessunDorma님// 45도는 상관없습니다. 45의 의미는 시간이 같을때 45도로 던질때가 거리가 가장 잘나간다는건데. 본문의 의미는 시간이 상수가 아니라 거리가 상수죠. 상식적으로 야구공 던지면 포물선 각이 적을수록 빨리 도착하죠. 그게 60도이든 45도이든 직선으로 던지든 말이죠. Vo가 같다면 높게 던지면 던질수록 수평거리는 짧아지죠. 수평거리를 늘리고 싶다 그럼 더 세게 던져서 Vo를 높이는 방법 밖에 없고요. [m]
13/03/30 16:46
아 그렇네요..NessunDorma 님도 과정은 모르겠지만 옳게 풀으셨겠죠. 제가 잘못 생각했습니다. 10년전에는 날라댕겼는데 나이를 먹으니 정말 굳어버렸네요, 머리가ㅜㅠ
13/03/30 16:46
제가 쓴 풀이는 도달거리가 같다는걸 이용한다는 겁니다.
(2V1^2*sinA*cosA)/g = (2V2^2*sinB*cosB)/g 에서 지울거 지우면 (V1*sinA)(V1*cosA) = (V2*sinB)(V2*cosB) 가 됩니다. 즉, 큰각도 던진것의 (수평속도 성분 x 수직속도성분) = 작은각도의 (수평속도 성분 x 수직속도성분 ) 이때 큰각도로 던진것의 수직속도 성분이 작은 각도로 던진것의 그것보다 크므로(h가 더 큽니다.) 식을 만족하려면 수평속도성분은 작은각도로 던진것이 더 크게 되죠. 도달 거리는 같은데 속도는 더 크다? 시간은 더 작게되는거죠. 말로 쓰니 좀 길어지네요 흐흐 다들 도움 주셔서 감사드립니다!
|
||||||||||||